搜索
【题目】如图，△ABC中，AB=5，BC=3，AC=4，以点C为圆心的圆与AB相切，则⊙C的半径为（ ）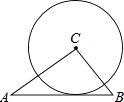 
A.2.3
B.2.4
C.2.5
D.2.6
参考答案：
【答案】B
【解析】解：在△ABC中，
∵AB=5，BC=3，AC=4，
∴AC2+BC2=32+42=52=AB2 ，
∴∠C=90°，
如图：设切点为D，连接CD，
∵AB是⊙C的切线，
∴CD⊥AB，
∵S△ABC= 
ACBC= ABCD，
∴ACBC=ABCD，
即CD= 
= 
= 
，
∴⊙C的半径为 ，
故选B．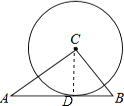
【考点精析】关于本题考查的切线的性质定理，需要了解切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，AE﹕EB=1﹕2，
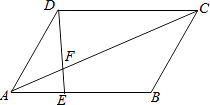
（1）求△AEF与△CDF的周长的比；
（2）如果S△AEF=5cm2 ， 求S△CDF ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AB=16cm，AD=6cm，动点P、Q分别从A、C两点同时出发，点P以3cm/s的速度向点B移动，一直到达点B为止，点Q以2cm/s的速度向点D移动．
（1）P、Q两点从出发开始，经过几秒时，四边形PBCQ的面积为33cm2？
（2）P、Q两点从出发开始，经过几秒时，点P和点Q的距离为10cm？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．
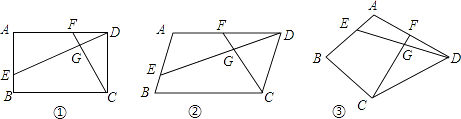
（1）如图①，若四边形ABCD是矩形，且DE⊥CF，求证：△ADE∽△DCF；
（2）如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，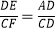
成立？并证明你的结论；
（3）如图③，若BA=BC=6，DA=DC=8，∠BAD=90°，DE⊥CF，请直接写出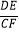
的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】在ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．
（1）如图1，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；
（2）如图2，当EF与AB相交时，若∠EAB=α（0°＜α＜90°），请你直接写出线段EG、AG、BG之间的数量关系（用含α的式子表示）；
（3）如图3，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）拼一拼，画一画：请你用4个长为a，宽为b的矩形拼成一个大正方形，并且正中间留下一个洞，这个洞恰好是一个小正方形。
（2）用不同方法计算中间的小正方形的面积，聪明的你能发现什么？
（3）当拼成的这个大正方形边长比中间小正方形边长多3cm时，它的面积就多24cm2，求中间小正方形的边长。
-
科目： 来源： 题型：
查看答案和解析>>【题目】小强的钱包内有10元钱、20元钱和50元钱的纸币各1张．
（1）若从中随机取出1张纸币，求取出纸币的金额是20元的概率；
（2）若从中随机取出2张纸币，求取出纸币的总额可购买一件51元的商品的概率．
相关试题
