【题目】如图所示，在△ABC中，AC=BC=4，∠C=90°，O是AB的中点，⊙O与AC、BC分别相切于点D、E，点F是⊙O与AB的一个交点，连接DF并延长交CB的延长线于点G，则BG的长是 ．

参考答案：

【答案】2 ﹣2
【解析】解：连接OD． ∵AC为圆O的切线，∴OD⊥AC，
又∵AC=BC=4，∠C=90°，
∴∠A=45°，
根据勾股定理得：AB= =4 ，
又∵O为AB的中点，
∴AO=BO= AB=2 ，
∴圆的半径DO=FO=AOsinA=2 × =2，
∴BF=OB﹣OF=2 ﹣2．
∵GC⊥AC，OD⊥AC，
∴OD∥CG，
∴∠ODF=∠G，
又∵∠OFD=∠BFG，
∴△ODF∽△BGF，
∴ ，即 = ，
∴BG=2 ﹣2．
故答案为：2 ﹣2．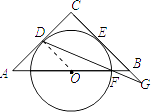

连接OD，由AC为圆O的切线，根据切线的性质得到OD与AC垂直，又AC=BC，且∠C=90°，得到三角形ABC为等腰直角三角形，得到∠A=45°，在直角三角形ABC中，由AC与BC的长，根据勾股定理求出AB的长，又O为AB的中点，从而得到AO等于BO都等于AB的一半，求出AO与BO的长，再由OB﹣OF求出FB的长，同时由OD和GC都与AC垂直，得到OD与GC平行，得到一对内错角相等，再加上对顶角相等，由两对对应角相等的两三角形相似得到三角形ODF与三角形GBF相似，由相似得比例，把OD，OF及FB的长代入即可求出GB的长．

关闭