【题目】如图,平面直角坐标系中,直线l:y=﹣ ![]() x+
x+ ![]() 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.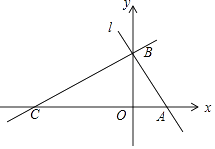
(1)求A,C两点的坐标.
(2)若点M从点C出发,以每秒1个单位长度的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,求出S关于t的函数关系式,并写出自变量的取值范围.
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A,B,P,Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
参考答案:
【答案】
(1)解:当x=0时,y= ![]() ;当y=0时,x=1.
;当y=0时,x=1.
∴点A坐标为(1,0),点B坐标为(0, ![]() ),
),
在Rt△BOC中,∠OCB=30°,OB= ![]() ,
,
∴BC=2 ![]() .
.
∴OC= ![]() =3.
=3.
∴点C坐标为(﹣3,0).
(2)解:如图1所示:
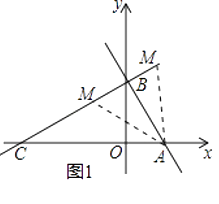
∵OA=1,OB= ![]() ,AB=2,
,AB=2,
∴∠ABO=30°,
同理:BC=2 ![]() ,∠OCB=30°,
,∠OCB=30°,
∴∠OBC=60°,
∴∠ABC=90°,
分两种情况考虑:若M在线段BC上时,BC=2 ![]() ,CM=t,可得BM=BC﹣CM=2
,CM=t,可得BM=BC﹣CM=2 ![]() ﹣t,
﹣t,
此时S△ABM= ![]() BMAB=
BMAB= ![]() ×(2
×(2 ![]() ﹣t)×2=2
﹣t)×2=2 ![]() ﹣t(0≤t<2
﹣t(0≤t<2 ![]() );
);
若M在BC延长线上时,BC=2 ![]() ,CM=t,可得BM=CM﹣BC=t﹣2
,CM=t,可得BM=CM﹣BC=t﹣2 ![]() ,
,
此时S△ABM= ![]() BMAB=
BMAB= ![]() ×(t﹣2
×(t﹣2 ![]() )×2=t﹣2
)×2=t﹣2 ![]() (t≥2
(t≥2 ![]() );
);
综上所述,S= ![]() ;
;
(3)解:P是y轴上的点,在坐标平面内存在点Q,使以 A、B、P、Q为顶点的四边形是菱形,
如2图所示,
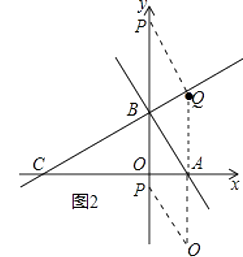
当P在y轴正半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A的横坐标相同,
此时Q坐标为(1,2),②AP=AQ= ![]() ,Q与A的横坐标相同,此时Q坐标为(1,
,Q与A的横坐标相同,此时Q坐标为(1, ![]() ),
),
当P在y轴负半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A横坐标相同,
此时Q坐标为(1,﹣2),②BP垂直平分AQ,此时Q坐标为(﹣1,0),
综上,满足题意Q坐标为(1,2)、(1,﹣2)、(1, ![]() )、(﹣1,0).
)、(﹣1,0).
【解析】(1)直线y=-![]() x+
x+![]() 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,当x=0时,y=
分别交x轴,y轴于A,B两点,点C在x轴负半轴上,当x=0时,y=![]() ;当y=0时,x=1;所以点A坐标为(1,0),点B坐标为(0,
;当y=0时,x=1;所以点A坐标为(1,0),点B坐标为(0, ![]() ),在Rt△BOC中,∠OCB=30°,OB=
),在Rt△BOC中,∠OCB=30°,OB=![]() ,得到BC=2
,得到BC=2![]() ,得到 OC=3,即点C坐标为(﹣3,0);(2)OA=1,OB=
,得到 OC=3,即点C坐标为(﹣3,0);(2)OA=1,OB=![]() ,AB=2,得到∠ABO=30°,同理:BC=2
,AB=2,得到∠ABO=30°,同理:BC=2![]() ,∠OCB=30°,得到∠OBC=60°,∠ABC=90°,分两种情况考虑:若M在线段BC上时,BC=2
,∠OCB=30°,得到∠OBC=60°,∠ABC=90°,分两种情况考虑:若M在线段BC上时,BC=2![]() ,CM=t,可得BM=BC﹣CM=2
,CM=t,可得BM=BC﹣CM=2![]() ﹣t,此时S△ABM=BMAB÷2=(2
﹣t,此时S△ABM=BMAB÷2=(2![]() ﹣t)×2÷2=2
﹣t)×2÷2=2![]() ﹣t(0≤t<2
﹣t(0≤t<2![]() );若M在BC延长线上时,BC=2
);若M在BC延长线上时,BC=2![]() ,CM=t,可得BM=CM﹣BC=t﹣2
,CM=t,可得BM=CM﹣BC=t﹣2 ![]() ,此时S△ABM=BMAB÷2=(t﹣2
,此时S△ABM=BMAB÷2=(t﹣2![]() )×2÷2=t﹣2
)×2÷2=t﹣2![]() (t≥2
(t≥2![]() );(3)当P在y轴正半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A的横坐标相同,此时Q坐标为(1,2),②AP=AQ= 2
);(3)当P在y轴正半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A的横坐标相同,此时Q坐标为(1,2),②AP=AQ= 2![]() ÷3 ,Q与A的横坐标相同,此时Q坐标为(1, 2
÷3 ,Q与A的横坐标相同,此时Q坐标为(1, 2![]() ÷3),当P在y轴负半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A横坐标相同,此时Q坐标为(1,﹣2),②BP垂直平分AQ,此时Q坐标为(﹣1,0),综上,满足题意Q坐标为(1,2)、(1,﹣2)、(1, 2
÷3),当P在y轴负半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A横坐标相同,此时Q坐标为(1,﹣2),②BP垂直平分AQ,此时Q坐标为(﹣1,0),综上,满足题意Q坐标为(1,2)、(1,﹣2)、(1, 2![]() ÷3 )、(﹣1,0).
÷3 )、(﹣1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型
目的地
A村(元/辆)
B村(元/辆)
大货车
800
900
小货车
400
600
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
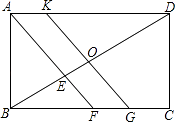
(1)求证:△DOK≌△BOG;
(2)探究线段AB、AK、BG三者之间的关系,并证明你的结论;
(3)若KD=KG,BC=2 ﹣1,求KD的长度.
﹣1,求KD的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】摩托车油箱中有8升油,行驶时每小时耗油2升,在不加油的情况下,求余油量Q(升)与行驶时间t(小时)之间的函数关系式为________,这里的时间t的取值范围为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】湛江市2009年平均房价为每平方米4000元.连续两年增长后,2011年平均房价达到每平方米5500元,设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
A.5500(1+x)2=4000
B.5500(1﹣x)2=4000
C.4000(1﹣x)2=5500
D.4000(1+x)2=5500 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,BC,AC,AB边的中点分别是点D,E,F,则下列说法可能不正确的为( )
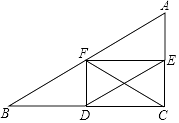
A.四边形CDFE是矩形
B.DE=CF= AB
AB
C.S△ABC=4S△AEF
D.∠B=30° -
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来根据以上信息,解答下列问题:
(1)设租车时间为
 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 元,分别求出
元,分别求出 ,
, 关于
关于 的函数表达式;
的函数表达式;(2)请你帮助小明计算并选择哪个出游方案合算。
相关试题

