【题目】如图,在Rt△ABC中,∠ACB=90°,BC,AC,AB边的中点分别是点D,E,F,则下列说法可能不正确的为( )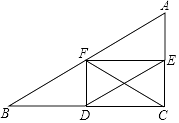
A.四边形CDFE是矩形
B.DE=CF= ![]() AB
AB
C.S△ABC=4S△AEF
D.∠B=30°
参考答案:
【答案】D
【解析】解:∵点D,E,F分别是BC,AC,AB的中点,
∴DF∥AC,EF∥BC,
∴四边形CDFE是平行四边形,
∵∠ACB=90°,
∴平行四边形CDFE是矩形,故A正确,
∴CF=DE,
∵点D,E是BC,AC中点,
∴DE= ![]() AB,
AB,
∴DE=CF= ![]() AB,
AB,
故B正确,
∵点E,F是AC,AB的中点,
∴EF= ![]() BC,EF∥BC,
BC,EF∥BC,
∴△AEF∽△ACB,
∴ ![]() =(
=( ![]() )2=
)2= ![]() ,
,
∴S△ABC=4S△AEF,
故C正确,
所以,A,B,C都正确,
即:不正确的只有D,
所以答案是:D.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对矩形的判定方法的理解,了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】摩托车油箱中有8升油,行驶时每小时耗油2升,在不加油的情况下,求余油量Q(升)与行驶时间t(小时)之间的函数关系式为________,这里的时间t的取值范围为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线l:y=﹣
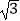 x+
x+ 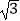 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.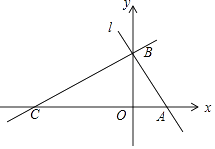
(1)求A,C两点的坐标.
(2)若点M从点C出发,以每秒1个单位长度的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,求出S关于t的函数关系式,并写出自变量的取值范围.
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A,B,P,Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】湛江市2009年平均房价为每平方米4000元.连续两年增长后,2011年平均房价达到每平方米5500元,设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
A.5500(1+x)2=4000
B.5500(1﹣x)2=4000
C.4000(1﹣x)2=5500
D.4000(1+x)2=5500 -
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
 [来
[来根据以上信息,解答下列问题:
(1)设租车时间为
 小时,租用甲公司的车所需费用为
小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为
元,租用乙公司的车所需费用为 元,分别求出
元,分别求出 ,
, 关于
关于 的函数表达式;
的函数表达式;(2)请你帮助小明计算并选择哪个出游方案合算。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
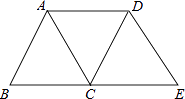
A.AB=BC
B.AC=BC
C.∠B=60°
D.∠ACB=60° -
科目: 来源: 题型:
查看答案和解析>>【题目】解关于x的方程:15x+9=8x-5
相关试题

