【题目】如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.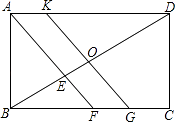
(1)求证:△DOK≌△BOG;
(2)探究线段AB、AK、BG三者之间的关系,并证明你的结论;
(3)若KD=KG,BC=2 ![]() ﹣1,求KD的长度.
﹣1,求KD的长度.
参考答案:
【答案】
(1)证明:∵在矩形ABCD中,AD∥BC,
∴∠KDO=∠GBO,∠DKO=BGO.
∵点O是BD的中点;
∴DO=BO.
在△DOK和△BOG中, 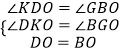
∴△DOK≌△BOG(AAS).
(2)解:AB+AK=BG;证明如下:
∵四边形ABCD是矩形;
∴∠BAD=∠ABC=90°,AD∥BC.
又∵AF平分∠BAD,
∴∠BAF=∠BFA=45°.
∴AB=BF.
∵OK∥AF,AK∥FG,
∴四边形AFGK是平行四边形.
∴AK=FG.
∵BG=BF+FG;
∴BG=AB+AK.
(3)解:∵四边形AFGK是平行四边形.
∴AK=FG,AF=KG
又∵△DOK≌△BOG,且KD=KG,
∴AF=KG=KD=BG.
设AB=a,则AF=KG=KD=BG= ![]() a.
a.
∴AK=2 ![]() ﹣1﹣
﹣1﹣ ![]() a,FG=BG﹣BF=
a,FG=BG﹣BF= ![]() a﹣a.
a﹣a.
∴2 ![]() ﹣1﹣
﹣1﹣ ![]() a=
a= ![]() a﹣a.
a﹣a.
解得a=1.
∴KD= ![]() a=
a= ![]() .
.
【解析】(1)在矩形ABCD中,AD∥BC,得到∠KDO=∠GBO,∠DKO=BGO,DO=BO,得到△DOK≌△BOG(AAS);(2)四边形ABCD是矩形,得到∠BAD=∠ABC=90°,AD∥BC,又AF平分∠BAD,得到∠BAF=∠BFA=45°,AB=BF,由OK∥AF,AK∥FG,得到四边形AFGK是平行四边形,得到AK=FG,BG=BF+FG,即BG=AB+AK;(3)四边形AFGK是平行四边形,得到AK=FG,AF=KG,又△DOK≌△BOG,且KD=KG,得到AF=KG=KD=BG,设AB=a,则AF=KG=KD=BG=![]() a,得到AK=2
a,得到AK=2![]() ﹣1-
﹣1-![]() a,FG=BG﹣BF=
a,FG=BG﹣BF=![]() a﹣a,解得a=1,得到KD=
a﹣a,解得a=1,得到KD=![]() a=
a=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】昌平万亩滨河森林公园占地3 980 000平方米,位于北京城市中轴线的北延线上,将北京城与十三陵水库通过绿轴有机地联系在一起,是名副其实的北京的“后花园”.把数字3 980 000用科学记数法表示为( )
A.39.8×105
B.3.98×106
C.3.98×107
D.0.398×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于
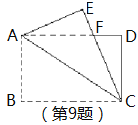
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型
目的地
A村(元/辆)
B村(元/辆)
大货车
800
900
小货车
400
600
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】摩托车油箱中有8升油,行驶时每小时耗油2升,在不加油的情况下,求余油量Q(升)与行驶时间t(小时)之间的函数关系式为________,这里的时间t的取值范围为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线l:y=﹣
 x+
x+ 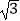 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.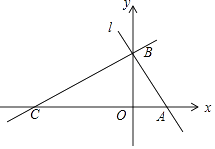
(1)求A,C两点的坐标.
(2)若点M从点C出发,以每秒1个单位长度的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,求出S关于t的函数关系式,并写出自变量的取值范围.
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A,B,P,Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】湛江市2009年平均房价为每平方米4000元.连续两年增长后,2011年平均房价达到每平方米5500元,设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
A.5500(1+x)2=4000
B.5500(1﹣x)2=4000
C.4000(1﹣x)2=5500
D.4000(1+x)2=5500
相关试题

