搜索
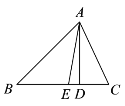
【题目】如图，在△ABC 中，∠C=65°，AD 为 BC 边上的高.
（1）求∠CAD 的度数；
（2）若∠B=45°，AE 平分∠BAC，求∠EAD 的度数.
参考答案：
【答案】（1）25°；（2）10°.
【解析】
根据直角三角形两锐角互余可得∠CAD=90°-∠C,再利用三角形的内角和定理求出∠BAC,根据角平分线的定义求出∠CAE,然后根据∠EAD=∠CAE-∠CAD计算即可得解.
（1）∵AD为BC边上的高
∴∠ADC=90°，
又∠C=65°，
∴∠CAD=90°-65°=25°，
（2）∵∠B=45°，∠C=65°，
∴∠BAC=180°-45°-65°=70°，
∵AE平分∠BAC，
∴∠CAE=
∠BAC=35°，
∴∠EAD=∠EAC-∠CAD=35°-25°=10°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知OA⊥OB，∠AOD=∠BOC由此判定OC⊥OD，下面是推理过程，请填空.
解：∵OA⊥OB(已知)
所以_____=90°（________）
因为_____=∠AOD-∠AOC，____=∠BOC-∠AOC，∠AOD=∠BOC，
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
-
科目： 来源： 题型：
查看答案和解析>>【题目】目前，步行已成为人们最喜爱的健身方法之一，通过手机可以计算行走的步数与相应的能量消耗．对比手机数据发现：小琼步行13500步与小刚步行9000步消耗的能量相同，若每消耗1千卡能量小琼行走的步数比小刚多15步，求小刚每消耗1千卡能量需要行走多少步？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABC中，AB=AC，∠BAC=90°，BE⊥CE，垂足是E，BE交AC于点D，F是BE上一点，AF⊥AE，且C是线段AF的垂直平分线上的点，AF=2
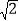，则DF=________.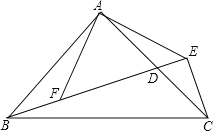
-
科目： 来源： 题型：
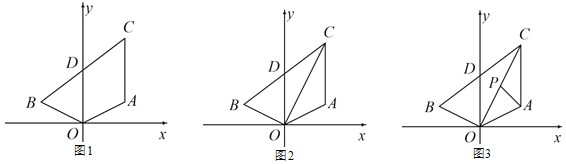
查看答案和解析>>【题目】如图 1，点 A(2，1)，点 A 与点 B 关于 y 轴对称，AC∥y 轴，且 AC=3，连接 BC 交 y 轴于点 D.
（1）点 B 的坐标为_____，点 C 的坐标为_____；
（2）如图 2，连接 OC，OC 平分∠ACB，求证：OB⊥OC；
（3）如图 3，在（2）的条件下，点 P 为 OC 上一点，且∠PAC=45°，求点 P 的坐标.
-
科目： 来源： 题型：
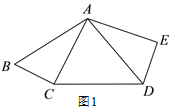
查看答案和解析>>【题目】如图 1，在五边形 ABCDE 中，∠E=90°，BC=DE.连接 AC，AD， 且 AB=AD，AC⊥BC.
（1）求证：AC=AE；
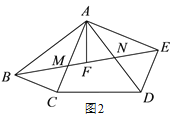
（2）如图 2，若∠ABC=∠CAD，AF 为 BE 边上的中线，求证：AF⊥CD；
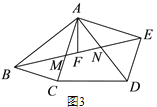
（3）如图 3，在（2）的条件下，AE=6，DE=4，则五边形 ABCDE 的面积为_____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB，CD 相交于点O，∠AOD=3∠BOD+20°.
(1)求∠BOD的度数；
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD，且∠EOF= 90°，求∠BOF的度数.
相关试题
