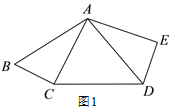
【题目】如图 1,在五边形 ABCDE 中,∠E=90°,BC=DE.连接 AC,AD, 且 AB=AD,AC⊥BC.
(1)求证:AC=AE;
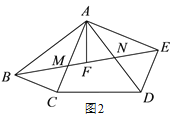
(2)如图 2,若∠ABC=∠CAD,AF 为 BE 边上的中线,求证:AF⊥CD;
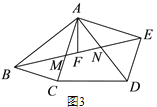
(3)如图 3,在(2)的条件下,AE=6,DE=4,则五边形 ABCDE 的面积为_____.
参考答案:
【答案】(1)见解析;(2)见解析;(3)42
【解析】
(1)由已知可得Rt△ABC≌Rt△ADE(HL),可得结论;
(2)延长 AF,BC 交于点 G,连接CG,可得∠G=∠EAG,可证明得:△AEF≌△GBF(AAS),可得AE=BG,∠ABG=∠CAD,可证明得△ABG≌△DAC(SAS),∠G=∠ACD,可得结论;
(3) 在(2)的条件下,AE=6,DE=4,则五边形 ABCDE 的面积为42.
(1)∵AC⊥BC,,
∴∠ACB=90°=∠E. 在 Rt△ABC 和 Rt△ADE 中,
AB AD,BC DE,
∴Rt△ABC≌Rt△ADE(HL),
∴AC=AE.
(2)延长 AF,BC 交于点 G,
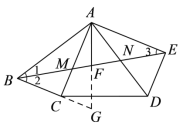
∵∠ABC=∠CAD,∠BAC=∠DAE,
∴∠CAD+∠DAE=∠ABC+∠BAC=90°=∠ACB,,
∴BG∥AE,
∴∠G=∠EAG,
在△AEF 和△GBF 中,
AFE GFB,EAF G,EF BF,
∴△AEF≌△GBF(AAS),
∴AE=BG,
∵AC= AE,
∴BG=AC.
∵∠2=∠3,
又∠ABG=∠1+∠2,
∠CAD=∠BAD+∠CAE-∠BAE,,
=180-∠BAE=180-(180-∠1-∠3)=∠1+∠3,
∴∠ABG=∠CAD,
在△ABG 和△DAC 中,
AB AD,ABG DAC,BG AC,
∴△ABG≌△DAC(SAS),
∴∠G=∠ACD,
∵∠ACG=∠ACB= 90° 即:∠ACD+∠GCD=90°,
∴∠G+∠GCD=90°,
∴AF⊥CD;
(3)在(2)的条件下,AE=6,DE=4,则五边形 ABCDE 的面积为42 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,BE⊥CE,垂足是E,BE交AC于点D,F是BE上一点,AF⊥AE,且C是线段AF的垂直平分线上的点,AF=2
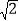 ,则DF=________.
,则DF=________.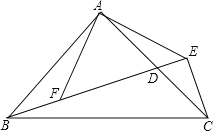
-
科目: 来源: 题型:
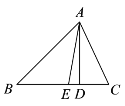
查看答案和解析>>【题目】如图,在△ABC 中,∠C=65°,AD 为 BC 边上的高.
(1)求∠CAD 的度数;
(2)若∠B=45°,AE 平分∠BAC,求∠EAD 的度数.
-
科目: 来源: 题型:
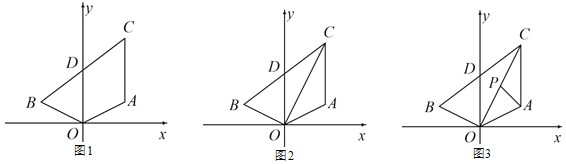
查看答案和解析>>【题目】如图 1,点 A(2,1),点 A 与点 B 关于 y 轴对称,AC∥y 轴,且 AC=3,连接 BC 交 y 轴于点 D.
(1)点 B 的坐标为_____,点 C 的坐标为_____;
(2)如图 2,连接 OC,OC 平分∠ACB,求证:OB⊥OC;
(3)如图 3,在(2)的条件下,点 P 为 OC 上一点,且∠PAC=45°,求点 P 的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,PB、PC分别是⊙O的切线,切点为B、C,PC、BA的延长线交于点D,DE⊥PO,交PO的延长线于点E.
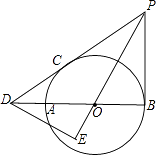
(1)求证:∠DPO=∠EDB;
(2)若PB=3,DB=4,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD是正方形,动点P从点A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止;动点Q从A出发,以1cm/s的速度沿边AD匀速运动到D终止,若P、Q两点同时出发,运动时间为ts,△APQ的面积为Scm2 . S与t之间函数关系的图象如图2所示.
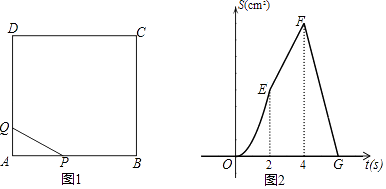
(1)求图2中线段FG所表示的函数关系式;
(2)当动点P在边AB运动的过程中,若以C、P、Q为顶点的三角形是等腰三角形,求t的值;
(3)是否存在这样的t,使PQ将正方形ABCD的面积恰好分成1:3的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
相关试题

