【题目】如图1,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.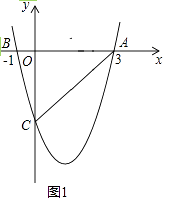
(1)求该二次函数的解析式及点C的坐标;
(2)设该抛物线的顶点为D,求△ACD的面积;
(3)若点P,Q同时从A点出发,如图2(注:图2与图1完全相同),都以每秒1个单位长度的速度分别沿线段AB,AC运动,当其中一点到达终点时,另一点也随之停止运动,当P,Q运动到t秒时,将△APQ沿PQ所在直线翻折,点A恰好落在抛物线上E处,判定此时四边形APEQ的形状,说明理由,并求出点E的坐标.
参考答案:
【答案】
(1)
解:把点A(3,0),B(﹣1,0)代入y=ax2+bx﹣4(a≠0)得:
![]() ,
,
解得: 
(2)
解:过点D作DM⊥y轴于点M,

∵y= ![]() x2﹣
x2﹣ ![]() x﹣4=
x﹣4= ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]() ,
,
∴点D(1,﹣ ![]() )、点C(0,﹣4),
)、点C(0,﹣4),
则S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC
= ![]() ×(1+3)×
×(1+3)× ![]() ﹣
﹣ ![]() ×(
×( ![]() ﹣4)×1﹣
﹣4)×1﹣ ![]() ×3×4
×3×4
=4
(3)
解:四边形APEQ为菱形,E点坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).理由如下
).理由如下
如图2,E点关于PQ与A点对称,过点Q作,QF⊥AP于F,

∵AP=AQ=t,AP=EP,AQ=EQ
∴AP=AQ=QE=EP,
∴四边形AQEP为菱形,
∵FQ∥OC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]()
∴AF= ![]() t,FQ=
t,FQ= ![]() t
t
∴Q(3﹣ ![]() t,﹣
t,﹣ ![]() t),
t),
∵EQ=AP=t,
∴E(3﹣ ![]() t﹣t,﹣
t﹣t,﹣ ![]() t),即E(3﹣
t),即E(3﹣ ![]() t,﹣
t,﹣ ![]() t),
t),
∵E在二次函数y= ![]() x2﹣
x2﹣ ![]() x﹣4上,
x﹣4上,
∴﹣ ![]() t=
t= ![]() (3﹣
(3﹣ ![]() t)2﹣
t)2﹣ ![]() (3﹣
(3﹣ ![]() t)﹣4,
t)﹣4,
∴t= ![]() ,或t=0(与A重合,舍去),
,或t=0(与A重合,舍去),
则3﹣ ![]() t=﹣
t=﹣ ![]() ,﹣
,﹣ ![]() t=﹣
t=﹣ ![]() ,
,
∴E(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)将A,B点坐标代入函数y=ax2+bx﹣4中,求得b、a,进而可求解析式;(2)由解析式先求得点D、C坐标,再根据S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC , 列式计算即可;(3)注意到P,Q运动速度相同,则△APQ运动时都为等腰三角形,又由A、E对称,则AP=EP,AQ=EQ,易得四边形四边都相等,即菱形.利用菱形对边平行且相等的性质可用t表示E点坐标,又E在二次函数的图象上,所以代入即可求t,进而E可表示.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数直方图和扇形统计图.
根据图中提供的信息,解答下列问题:
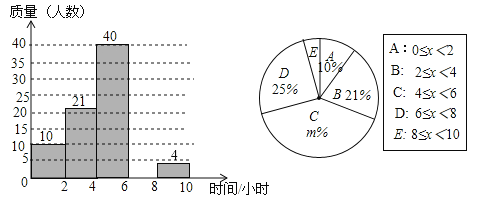
(1)补全频数直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)被调查的学生每周的课外阅读时间的众数落在哪一个范围内?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C为⊙O上一点,点D是弧BC的中点,DE⊥AC于点E,DE⊥AB于点F.

(1)求证:DE是⊙O的切线;
(2)若OF=2,求AC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接常熟市文明城市创建工作,某校八年一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为
 、
、 、
、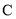 、
、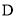 四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:(1)求八年一班共有多少人;
(2)补全折线统计图;
(3)在扇形统计图中等极为“
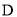 ”的部分所占圆心角的度数为 ;
”的部分所占圆心角的度数为 ;(4)若等级
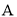 为优秀,求该班的优秀率。
为优秀,求该班的优秀率。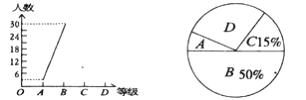
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)
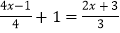
(2)
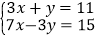
(3)
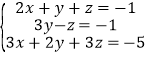
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了考查一种零件的加工精度,从中抽出40只进行检测,其尺寸数据如下(单位:微米):
161,165,164,166,160,158,163,162,168,159,
147,165,167,151,164,159,152,159,149,172,
162,157,162,169,156,164,163,157,163,165,
173,159,157,169,165,154,153,163,168,169.
试列出样本频数及频率分布表,绘制频数分布直方图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
相关试题

