【题目】如图,△ABC与△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,连接BE,将BE绕点B顺时针旋转90°,得BF,连接AD,BD,AF
(1)如图①,D、E分别在AC,BC边上,求证:四边形ADBF为平行四边形;
(2)△DEC绕点C逆时针旋转,其它条件不变,如图②,(1)的结论是否成立?说明理由.
(3)在图①中,将△DEC绕点C逆时针旋转一周,其它条件不变,问:旋转角为多少度时.四边形ADBF为菱形?直接写出旋转角的度数.

参考答案:
【答案】(1)见解析;(2)见解析;(3)旋转角为135°或315°时,四边形ADBF为菱形,理由见解析.
【解析】试题分析:(1)先根据△ABC与△DEC均为等腰直角三角形,以及旋转的性质,得出AD=BE,AD∥BF,进而得到四边形![]() 为平行四边形;
为平行四边形;
(2)先延长BE交AD于G,交AC于O,根据△ABC与△DEC均为等腰直角三角形,判定△ACD≌△BCE(SAS),得出AD=BE,∠CAD=∠CBE,再根据“8字形”得出∠AGE=90°,判定AD∥BF,即可得出四边形![]() 为平行四边形;
为平行四边形;
(3)分两种情况讨论:当旋转角![]() 时,当旋转角为
时,当旋转角为![]() 时,分别判定△ACD≌△BCD,得到
时,分别判定△ACD≌△BCD,得到![]() 再根据四边形
再根据四边形![]() 为平行四边形,得出四边形
为平行四边形,得出四边形![]() 为菱形.
为菱形.
试题解析:(1)如图1,∵△ABC与△DEC均为等腰直角三角形,

∴AC-DC=BC-EC,
∴AD=BE,
∵将BE绕点B顺时针旋转90°得BF,
∴BE=BF,
∴AD=BF,
又∵∠ACB=90°,∠CBF=90°,
∴∠C+∠CBF=180°,
∴AD∥BF,
∴四边形ADBF为平行四边形;
(2)如图2,(1)中的结论仍成立.
理由:延长BE交AD于G,交AC于O,
∵△ABC与△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,
∴DC=EC,AC=BC,∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
又∵BE=BF,∠ACB=90°,∠AOG=∠BOC,
∴AD=BF,∠AGE=90°,
∠AGB+∠EBF=180°,
∴AD∥BF,
∴四边形ADBF为平行四边形;

(3)旋转角为135°或315°时,四边形ADBF为菱形.
理由:如图所示,当旋转角∠BCE=135°时,∠ACE=45°,此时∠BCD=135°,
∴∠ACD=∠BCD,
又∵AC=BC,
∴△ACD≌△BCD(SAS),
∴AD=BD,
又∵四边形ADBF为平行四边形,
∴四边形ADBF为菱形;
如图所示,当旋转角为315°时,∠BCE=45°,此时∠BCD=45°,
∵∠ACB=90°,
∴∠ACD=∠BCD,
又∵AC=BC,
∴△ACD≌△BCD(SAS),
∴AD=BD,
又∵四边形ADBF为平行四边形,
∴四边形ADBF为菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC,BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用小立方体搭成一个几何体,从正面和上面看到该几何体的形状图如图所示,搭建这样的几何体最多要几个小立方体?最少要几个小立方体?并画出最多和最少时从左面看到的形状图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.

(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
图形
①
②
③
④
顶点数(V)
边数(E)
区域数(F)
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
 ;
;(2)
 ;
;(3)
 ;
; (4)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】方程
 的解为
的解为
 的解为
的解为
 的解为
的解为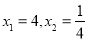 ;……根据发现的规律:
;……根据发现的规律:(1)请写出第7个方程:___________,它的解为x1=____________ , x2=____________.
(2)请写出第(n-1)个方程:____________,它的解为x1=____________, x2=____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣4x与x轴交于点O,A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )

A.4
B.8
C.16
D.32
相关试题

