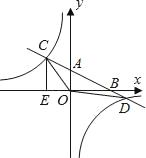
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
参考答案:
【答案】(1)y=﹣![]() x+2,y=﹣
x+2,y=﹣![]() .(2)8.
.(2)8.
【解析】试题分析:(1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例的函数解析式;
(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解.
试题解析:(1)∵OB=4,OE=2,
∴BE=2+4=6.
∵CE⊥x轴于点E,tan∠ABO=![]() .
.
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(-2,3).
设直线AB的解析式为y=kx+b,则![]() ,
,
解得 .
.
故直线AB的解析式为y=-![]() x+2.
x+2.
设反比例函数的解析式为y=![]() (m≠0),
(m≠0),
将点C的坐标代入,得3=![]() ,
,
∴m=-6.
∴该反比例函数的解析式为y=-![]() .
.
(2)联立反比例函数的解析式和直线AB的解析式可得
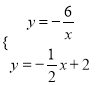 ,
,
可得交点D的坐标为(6,-1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学兴趣小组为了解我校初三年级1800名学生的身体健康情况,从初三随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
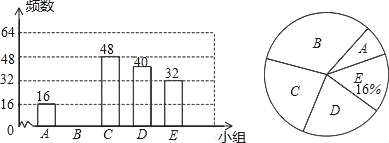
补全条形统计图,并估计我校初三年级体重介于47kg至53kg的学生大约有多少名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①﹣|﹣2|和﹣(﹣2)互为相反数;②绝对值等于它本身的数是0、1;③若
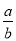 =﹣1则a、b为相反数;④﹣210读作“﹣2的10次幂”⑤近似数9.7万精确到十分位;⑥若a是有理数,则它的相反数是﹣a,倒数是
=﹣1则a、b为相反数;④﹣210读作“﹣2的10次幂”⑤近似数9.7万精确到十分位;⑥若a是有理数,则它的相反数是﹣a,倒数是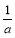 ;下列说法正确的是( )
;下列说法正确的是( )A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:数a,b,c 在数轴上的对应点如下图所示,
(1)在数轴上表示﹣a;
(2)比较大小(填“<”或“>”或“=”):a+b 0,﹣3c 0,c﹣a 0;
(3)化简|a+b|﹣|﹣3c|﹣|c﹣a|.

-
科目: 来源: 题型:
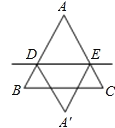
查看答案和解析>>【题目】如图,等边三角形ABC的边长为3,D、E分别是AB、AC上的点,且AD=AE=2,将△ADE沿直线DE折叠,点A的落点记为A′,则四边形ADA′E的面积S1与△ABC的面积S2之间的关系是( )
A.
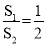 B.
B.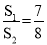 C.
C.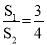 D.
D.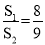
-
科目: 来源: 题型:
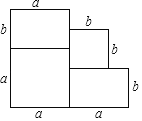
查看答案和解析>>【题目】如图是一所住宅的建筑平面图.
(1)用含有a、b的式子表示这所住宅的建筑面积.
(2)当a=5米,b=4米时,住宅的建筑面积有多大?
(3)在(2)的条件下,若此住宅的销售单价为每平方米5000元,求此住宅的销售价是多少元?(结果用科学记数法表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
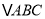 的两边
的两边 、
、 的长分别是关于x的一元二次方程
的长分别是关于x的一元二次方程 的两个实数根,第三边
的两个实数根,第三边 的长为5.
的长为5.(1)当
 为何值时,
为何值时,  是直角三角形;
是直角三角形;(2)当
 为何值时,
为何值时,  是等腰三角形,并求出
是等腰三角形,并求出 的周长.
的周长.
相关试题

