【题目】已知![]() 的两边
的两边![]() 、
、![]() 的长分别是关于x的一元二次方程
的长分别是关于x的一元二次方程![]() 的两个实数根,第三边
的两个实数根,第三边![]() 的长为5.
的长为5.
(1)当![]() 为何值时,
为何值时, ![]() 是直角三角形;
是直角三角形;
(2)当![]() 为何值时,
为何值时, ![]() 是等腰三角形,并求出
是等腰三角形,并求出![]() 的周长.
的周长.
参考答案:
【答案】(1)2;(2)14或6
【解析】试题分析:
(1)△ABC是以BC为斜边的直角三角形,即AB,AC的平方和是25,则一元二次方程x2-(2k+3)x+k2+3k+2=0的两个实数根的平方和是25,根据韦达定理和勾股定理解出k的值,再把k的值代入原方程,检查k是哪个值时,△ABC是以BC为斜边的直角三角形则可;(2)根据等腰三角形的性质,分三种情况讨论:①AB=AC,②AB=BC,③BC=AC;后两种情况相同,则可有另种情况,再由根与系数的关系得出k的值,再求![]() 的周长。
的周长。
试题解析:
(1)设边AB=a,AC=b
∵a、b是方程x2-(2k+3)x+k2+3k+2=0的两根
∴a+b=2k+3,a-b=k2+3k+2
又∵△ABC是以BC为斜边的直角三角形,且BC=5
∴a2+b2=52,
即(a+b)2-2ab=52,
∴(2k+3)2-2(k2+3k+2)=25
∴k2+3k-10=0
∴k1=-5或k2=2
当k=-5时,方程为:x2+7x+12=0
解得:x1=-3,x2=-4(舍去)
当k=2时,方程为:x2-7x+12=0
解得:x1=3,x2=4
∴当k=2时,△ABC是以BC为斜边的直角三角形.
(2)∵△ABC是等腰三角形;
∴当AB=AC时,△=b2-4ac=0,
∴(2k+3)2-4(k2+3k+2)=0
解得k不存在;
当AB=BC时,即AB=5,
∴5+AC=2k+3,5AC=k2+3k+2,
解得k=3或4,
∴AC=4或6,
∴△ABC的周长为14或16
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人各用一张正方形的纸片ABCD折出一个45°的角(如图),两人做法如下:
甲:将纸片沿对角线AC折叠,使B点落在D点上,则∠1=45°;
乙:将纸片沿AM、AN折叠,分别使B、D落在对角线AC上的一点P,则∠MAN=45°.
对于两人的做法,下列判断正确的是( )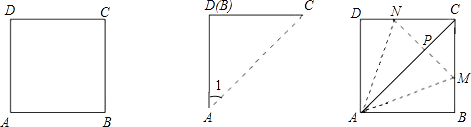
A.甲乙都对
B.甲对乙错
C.甲错乙对
D.甲乙都错 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)10+4(x﹣3)=2x﹣1;
(2)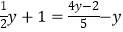 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一抛物线型的立交桥桥拱,这个桥拱的最大高度为16米,跨度为40米,若要在跨度中心点
 的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?
的左,右5米处各垂直竖立一根铁柱支撑拱顶,则铁柱应取多长?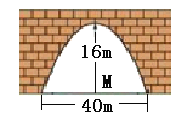
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a3·a5=________,x5·x=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线在平面直角坐标系中与y轴交于点A,点B(﹣3,3)也在直线上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C也在直线上.求点A的坐标和直线的解析式;
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式3ab2-2ab-1的次数为。
相关试题

