【题目】每年11月的最后一个星期四是感恩节,小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人.他将调查结果分为如下四类:A类﹣﹣当面致谢;B类﹣﹣打电话;C类﹣﹣发短信息或微信;D类﹣﹣写书信.他将调查结果绘制成如图不完整的扇形统计图和条形统计图: 请你根据图中提供的信息完成下列各题: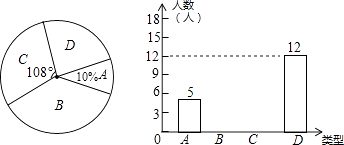
(1)补全条形统计图;
(2)在A类的同学中,有3人来自同一班级,其中有1人学过主持.现准备从他们3人中随机抽出两位同学主持感恩节主题班会课,请你用树状图或表格求出抽出的两人都没有学过主持的概率.
参考答案:
【答案】
(1)解:由题意可知总人数=5÷10%=50(人),所以D类所占的百分比为12÷50×100%=24%,C所占的百分比= ![]() =30%,所以C所占的人数=50×30%=15(人);
=30%,所以C所占的人数=50×30%=15(人);
B所占的百分比=1﹣10%﹣24%﹣30%=36%,B所占的人数=50×36%=18(人),由此补全统计图可得:

(2)解:设两个没学过主持的学生别标记为A1,A2,学过主持的学生标记为B1,列表如下:
A1 | A2 | B1 | |
A1 | (A1,A2) | (A1,B1) | |
A2 | (A2,A1) | (A2,B1) | |
B1 | (B1,A1) | (B1,A2) |
P(两人都没有学过主持)= ![]() =
= ![]()
【解析】(1)首先由A类的人数和其所占的比例可求出总人数,进而可求出B,C所占的人数,继而可以不签统计图;(2)设两个没学过主持的学生别标记为A1,A2,学过主持的学生标记为B1,列出表格即可求出抽出的两人都没有学过主持的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=
 AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.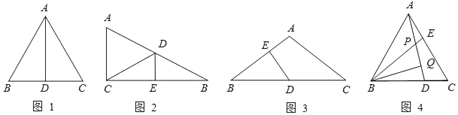
请根据从上面材料中所得到的信息解答下列问题:
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,求△ACD的周长.
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,求BE:EA的值.
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了“让世界充满爱”的捐款助学活动,其中八(2)班全体同学的捐款情况如下表:
捐款金额(元)
5
10
15
20
50
捐款人数(人)
7
18
12
3
由于填表的同学不小心把墨水滴在了表上,致使表中数据不完整,但知道捐款金额为10元的人数为全班人数的36%,结合上表回答下列问题:
(1)八(2)班共有多少人?
(2)学生捐款金额的众数和中位数分别为多少元?
(3)如果把该班学生的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对应的扇形圆心角为多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由梯子A B和梯子AC搭成的脚手架,其中AB=AC=5米,∠α=70°.

(1)求梯子顶端A离地面的高度AD的长和两梯脚之间的距离BC的长.
(2)生活经验告诉我们,增大两梯脚之间的距离可降低梯子的高度,若BC长达到6米,则梯子的高度下降多少米?(以上结果均精确到0.1米,供参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75) -
科目: 来源: 题型:
查看答案和解析>>【题目】微信运动和腾讯公益推出了一个爱心公益活动:一天中走路步数达到10000步及以上可通过微信运动和腾讯基金会向公益活动捐款,如果步数在10000步及以上,每步可捐0.0002元;若步数在10000步以下,则不能参与捐款.
(1)老赵某天的步数为13000步,则他当日可捐多少钱?
(2)已知甲、乙、丙三人某天通过步数共捐了8.4元,且甲的步数=乙的步数=丙步数的3倍,则丙走了多少步?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
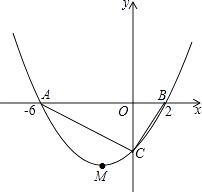
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
相关试题

