【题目】数学课堂探究性活动蔚然成风。张老师在课堂上设置一道习题:
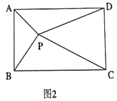
(1)已知矩形ABCD和点P,当点P在BC上任一位置(如图1所示)时,探究PA2、PB2、PC2、PD2,之间的关系?直接写出结论,不必证明;
当P点在其它位置时,请同学们分组探究:
(2)当点P在矩形内部,如图2时,探究PA2、PB2、PC2、PD2之间的数量关系,请你把探究出的结论写出来,并给予证明。
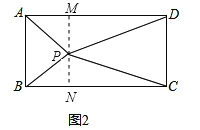
(3)当点P在矩形外部,如图3时,继续探完PA2、PB2、PC2、PD2之间的数量关系,请你把探究出的结论直接写出来,不必证明。


参考答案:
【答案】(1)(2)(3)结论PA2+PC2=PB2+PD2,证明见解析
【解析】试题分析:(1)直接根据勾股定理即可得出结论;
(2)过点P作MN⊥AD于点M,交BC于点N,可在Rt△AMP,Rt△BNP,Rt△DMP和Rt△CNP分别用勾股定理表示出PA2,PC2,PB2,PD2,然后我们可得出PA2+PC2与PB2+PD2,我们不难得出四边形MNCD是矩形,于是,MD=NC,AM=BN,然后我们将等式右边的值进行比较发现PA2+PC2=PB2+PD2.如图(3)方法同(2),过点P作PQ⊥BC交AD,BC于O,易证.
试题解析:证明:(1)如图1中.在Rt△ABP中,AB2=AP2﹣BP2,Rt△PDC中,CD2=PD2﹣PC2.∵AB=CD,∴AP2﹣BP2=PD2﹣PC2,∴PA2+PC2=PB2+PD2;
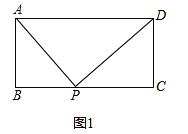
(2)猜想:PA2+PC2=PB2+PD2.
如图2,过点P作MN⊥AD于点M,交BC于点N.
在矩形ABCD中,∵AD∥BC,MN⊥AD,∴MN⊥BC.在Rt△AMP中, PA2=PM2+MA2.在Rt△BNP中,PB2=PN2+BN2.在Rt△DMP中,PD2=DM2+PM2.在Rt△CNP中,PC2=PN2+NC2,∴PA2+PC2=PM2+MA2+PN2+NC2,PB2+PD2=PM2+DM2+BN2+PN2.∵MN⊥AD,MN⊥NC,DC⊥BC,∴四边形MNCD是矩形,∴MD=NC,同理AM=BN,∴PM2+MA2+PN2+NC2=PM2+DM2+BN2+PN2,即PA2+PC2=PB2+PD2.
(3)如图3,过点P作PQ⊥BC交AD,BC于O,Q.

∵在矩形ABCD中,AD∥BC,PQ⊥BC,∴PQ⊥AD.∵在Rt△AOP中,PA2=AO2+PO2.在Rt△PQB中,PB2=PQ2+QB2.在Rt△POD中,PD2=DO2+PO2.在Rt△CQP中,PC2=PQ2+QC2,∴PA2+PC2=PO2+OA2+PQ2+QC2,PB2+PD2=PQ2+QB2+DO2+PO2.∵PQ⊥AD,PQ⊥NC,DC⊥BC,∴四边形OQCD是矩形,∴OD=QC,同理AO=BQ,∴PA2+PC2=PB2+PD2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第15次“移位”后,则他所处顶点的编号为__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从超市出发,向东走了3km,到达小刚家,继续向东走了4km到达小红家,又向西走了11km到达小英家,最后回到超市。
(1)请以超市为原点,以向东方向为正方向,用1个单位长度表示1km,画出数轴。并在数轴上表示出小刚家、小红家、小英家的位置;
(2)小英家距小刚家有多远?
(3)货车一共行驶了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点O(0,0),A(2,1),抛物线
 :
:  (h为常数)与y轴的交点为B.
(h为常数)与y轴的交点为B.(1)若t经过点A,求它的解析式,并写出此时t的对称轴及顶点坐标;
(2)设点B的纵坐标
 ,求
,求 的最大值,此时
的最大值,此时 上有两点(
上有两点( ),(
),( ),其中
),其中 >
> ,比较
,比较 与
与 的大.
的大.
-
科目: 来源: 题型:
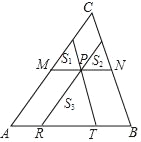
查看答案和解析>>【题目】如图,已知P为△ABC内一点,过P点分别作直线平行于△ABC的各边,形成小三角形的面积S1、S2、S3,分别为4、9、49,则△ABC的面积为_____.
-
科目: 来源: 题型:
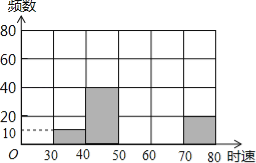
查看答案和解析>>【题目】将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):
数据段
30~40
40~50
50~60
60~70
70~80
总计
频 数
10
40
20
百分比
5%
40%
10%
注:30~40为时速大于等于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段汽车时速超过60千米即为违章,则违章车辆共有多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个平行四边形的一个内角的平分线分它的一边为1:2两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”,当协调边为6时,它的周长为______
相关试题

