【题目】如图,已知二次函数![]() 的图象的顶点为A.二次函数
的图象的顶点为A.二次函数![]() 的图象与x轴交于原点O及另一点C,它的顶点B在函数
的图象与x轴交于原点O及另一点C,它的顶点B在函数![]() 的图象的对称轴上.
的图象的对称轴上.
(1)求点A与点C的坐标;
(2)当四边形AOBC为菱形时,求函数![]() 的关系式.
的关系式.

参考答案:
【答案】(1)C(2,0);(2)![]() .
.
【解析】试题分析:(1)二次函数y=ax2+bx的顶点在已知二次函数抛物线的对称轴上,可知两个函数对称轴相等,因此先根据已知函数求出对称轴.根据函数解析式得出顶点A的坐标与对称轴,故可得出二次函数y=ax2+bx关于x=1对称,且函数与x轴的交点分别是原点和C点,所以点C和点O关于直线l对称,故可得出点C的坐标;
(2)因为四边形AOBC是菱形,根据菱形性质,可以得出点O和点C关于直线AB对称,点B和点A关于直线OC对称,因此,可求出点B的坐标,根据二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),将B,C代入解析式得出ab的值,进而得出其解析式.
试题解析:(1)∵y=x2-2x-1=(x-1)2-2,
∴顶点A的坐标为(1,-2).
∵二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
∴二次函数y=ax2+bx的对称轴为:直线x=1,
∴点C和点O关于直线x=1对称,
∴点C的坐标为(2,0).
(2)因为四边形AOBC是菱形,所以点B和点A关于直线OC对称,
因此,点B的坐标为(1,2).
因为二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),
所以![]()
解得![]() ,
,
所以二次函数y=ax2+bx的关系式为y=-2x2+4x.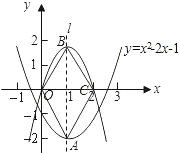
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 ,且
,且 ,
, 满足
满足 .过点
.过点 分别作
分别作 轴、
轴、 轴,垂足分别是点
轴,垂足分别是点 、
、 .
.

(1)求出点
 的坐标;
的坐标;(2)点
 是边
是边 上的一个动点(不与点
上的一个动点(不与点 重合),
重合), 的角平分线交射线
的角平分线交射线 于点
于点 ,在点
,在点 运动过程中,
运动过程中,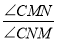 的值是否变化?若不变,求出其值;若变化,说明理由.
的值是否变化?若不变,求出其值;若变化,说明理由.(3)在四边形
 的边上是否存在点
的边上是否存在点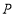 ,使得
,使得 将四边形
将四边形 分成面积比为1:4的两部分?若存在,请直接写出点
分成面积比为1:4的两部分?若存在,请直接写出点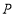 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交与A(1,0),B(- 3,0)两点
与x轴交与A(1,0),B(- 3,0)两点(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某图书借阅室提供两种租书方式:一种是零星租书,每册收费 1 元;另一种是会员租书,会员卡费用为每季度10 元,租书费每册 0.5 元.小亮经常来租书,若每季度租书数量为 x 册.
(1)写出零星租书方式每季度应付金额 y1(元)与租书数量 x(册)之间的函数关系式;
(2)写出会员卡租书方式每季度应付金额 y2(元)与租书数量 x(册)之间的函数关系式;
(3)请分析小亮选取哪种租书方式更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥的高为3
 cm,侧面展开图是半圆,
cm,侧面展开图是半圆,求:(1)圆锥母线与底面半径的比;
(2)锥角的大小;
(3)圆锥的全面积.
相关试题

