【题目】某图书借阅室提供两种租书方式:一种是零星租书,每册收费 1 元;另一种是会员租书,会员卡费用为每季度10 元,租书费每册 0.5 元.小亮经常来租书,若每季度租书数量为 x 册.
(1)写出零星租书方式每季度应付金额 y1(元)与租书数量 x(册)之间的函数关系式;
(2)写出会员卡租书方式每季度应付金额 y2(元)与租书数量 x(册)之间的函数关系式;
(3)请分析小亮选取哪种租书方式更合算?
参考答案:
【答案】![]() ;
;![]() ;(3)当每季度租书少于20册时,采用零星租书合算;当每季度租书恰为20册时,两种方式费用相同;当每季度租书多于20册时,会员租书方式更合算.
;(3)当每季度租书少于20册时,采用零星租书合算;当每季度租书恰为20册时,两种方式费用相同;当每季度租书多于20册时,会员租书方式更合算.
【解析】
(1)根据题意即可写出零星租书方式每季度应付金额 y1(元)与租书数量 x(册)之间的函数关系式;
(2)根据题意即可写出会员卡租书方式每季度应付金额 y2(元)与租书数量 x(册)之间的函数关系式;
(3)令y1= y2,求出此时的租书数,即可求解.
(1)零星租书方式每季度应付金额 y1(元)与租书数量 x(册)之间的函数关系式为![]() ;
;
(2)会员卡租书方式每季度应付金额 y2(元)与租书数量 x(册)之间的函数关系式为![]() ;
;
(3)当y1= y2,即x=0.5x+10
解得x=20
故:当每季度租书少于20册时,采用零星租书合算;
当每季度租书恰为20册时,两种方式费用相同;
当每季度租书多于20册时,会员租书方式更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交与A(1,0),B(- 3,0)两点
与x轴交与A(1,0),B(- 3,0)两点(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 的图象的顶点为A.二次函数
的图象的顶点为A.二次函数 的图象与x轴交于原点O及另一点C,它的顶点B在函数
的图象与x轴交于原点O及另一点C,它的顶点B在函数 的图象的对称轴上.
的图象的对称轴上.(1)求点A与点C的坐标;
(2)当四边形AOBC为菱形时,求函数
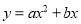 的关系式.
的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥的高为3
 cm,侧面展开图是半圆,
cm,侧面展开图是半圆,求:(1)圆锥母线与底面半径的比;
(2)锥角的大小;
(3)圆锥的全面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图),求光源离地面的垂直高度SO.(精确到0.1m;
 =1.44,
=1.44, =1.732,
=1.732, =2.236,以上数据供参考)
=2.236,以上数据供参考)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是______.

相关试题

