【题目】如图,已知点![]() ,且
,且![]() ,
,![]() 满足
满足![]() .过点
.过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴,垂足分别是点
轴,垂足分别是点![]() 、
、![]() .
.


(1)求出点![]() 的坐标;
的坐标;
(2)点![]() 是边
是边![]() 上的一个动点(不与点
上的一个动点(不与点![]() 重合),
重合),![]() 的角平分线交射线
的角平分线交射线![]() 于点
于点![]() ,在点
,在点![]() 运动过程中,
运动过程中,![]() 的值是否变化?若不变,求出其值;若变化,说明理由.
的值是否变化?若不变,求出其值;若变化,说明理由.
(3)在四边形![]() 的边上是否存在点
的边上是否存在点![]() ,使得
,使得![]() 将四边形
将四边形![]() 分成面积比为1:4的两部分?若存在,请直接写出点
分成面积比为1:4的两部分?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
参考答案:
【答案】(1)![]() 的坐标为
的坐标为![]() ;(2)不变化,
;(2)不变化,![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
【解析】
(1)由绝对值和算术平方根的性质可知![]() ,故两者和为0时,各自都必须为0,即
,故两者和为0时,各自都必须为0,即![]() ,由此可列出关于
,由此可列出关于![]() ,
,![]() 的二元一次方程组,解之即可得出B点坐标;(2)根据平行线和角平分线的性质可证明
的二元一次方程组,解之即可得出B点坐标;(2)根据平行线和角平分线的性质可证明![]() ,所以比值不变化;(3)点P只能在OC,OA边上,表示出两部分的面积,依比值求解即可.
,所以比值不变化;(3)点P只能在OC,OA边上,表示出两部分的面积,依比值求解即可.
解:(1)由![]() 得:
得:
![]() ,解得:
,解得:![]()
∴点![]() 的坐标为
的坐标为![]()
(2)不变化
∵ ![]() 轴
轴
∴BC∥x轴
∴ ![]()
∵ ![]() 平分
平分![]()
∴ ![]()
∴ ![]()
∴ ![]()
(3)点P可能在OC,OA边上,如下图所示,


由(1)可知,BC=5,AB=3,故矩形![]() 的面积为15
的面积为15
若点P在OC边上,可设P点坐标为![]() ,则
,则![]()
三角形BCP的面积为![]() ,
,
剩余部分面积为![]() ,
,
所以![]() ,解得
,解得![]() ,
,
P点坐标为![]() ;
;
若点P在OA边上,可设P点坐标为![]() ,则
,则![]()
三角形BAP的面积为![]() ,
,
剩余部分面积为![]() ,
,
所以![]() ,解得
,解得![]() ,
,
P点坐标为![]() .
.
综上,点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示8×7的正方形网格中,A(2,0),B(3,2),C(4,2),请按要求解答下列问题:

(1)将△ABO向右平移4个单位长度得到△A1B1O1,请画出△A1B1O1并写出点A1的坐标;
(2)将△ABO绕点C(4,2)顺时针旋转90°得到△A2B2O2,请画出△A2B2O2并写出点A2的坐标;
(3)将△A1B1O1绕点Q旋转90°可以和△A2B2O2完全重合,请直接写出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交与A(1,0),B(- 3,0)两点
与x轴交与A(1,0),B(- 3,0)两点(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 的图象的顶点为A.二次函数
的图象的顶点为A.二次函数 的图象与x轴交于原点O及另一点C,它的顶点B在函数
的图象与x轴交于原点O及另一点C,它的顶点B在函数 的图象的对称轴上.
的图象的对称轴上.(1)求点A与点C的坐标;
(2)当四边形AOBC为菱形时,求函数
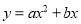 的关系式.
的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
相关试题

