搜索
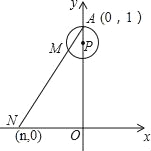
【题目】如图，在直角坐标系xOy中，已知点A（0，1），点P在线段OA上，以AP为半径的⊙P周长为1．点M从A开始沿⊙P按逆时针方向转动，射线AM交x轴于点N（n，0），设点M转过的路程为m（0＜m＜1）．
（1）当m=
时，n=_____；
（2）随着点M的转动，当m从
变化到
时，点N相应移动的路径长为_____．
参考答案：
【答案】 -1 
【解析】试题解析：（1）当m=
时，连接PM，如图1，
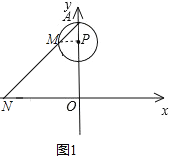
则有∠APM=×360°=90°．
∵PA=PM，∴∠PAM=∠PMA=45°．
∴NO=AO=1，
∴n=-1．
（2）①当m=
时，连接PM，如图2，
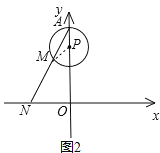
∠APM=×360°=120°．
∵PA=PM，∴∠PAM=∠PMA=30°．
在Rt△AON中，NO=AOtan∠OAN=1×
=；
②当m=
时，连接PM，如图3，
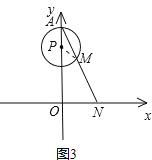
∠APM=360°-×360°=120°，
同理可得：NO=．
综合①、②可得：点N相应移动的路经长为+=．
故答案为．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个四位正整数m各个数位上的数字互不相同且都不为0，四位数m的前两位数字之和为5，后两位数字之和为11，称这样的四位数m为“半期数”；把四位数m的各位上的数字依次轮换后得到新的四位数m′，设m′＝
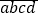，在m′的所有可能的情况中，当|b+2c﹣a﹣d|最小时，称此时的m′是m的“伴随数”，并规定F（m′）＝a2+c2﹣2bd；例如：m＝2365，则m′为：3652，6523，5236，因为|6+10﹣3﹣2|＝11，|5+4﹣6﹣3|＝0，|2+6﹣5﹣6|＝3，0最小，所以6523叫做2365的“伴随数”，F（5236）＝52+32﹣2×2×6＝10．（1）最大的四位“半期数”为 ；“半期数”3247的“伴随数”是 ．
（2）已知四位数P＝
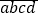是“半期数”，三位数Q＝
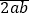，且441Q﹣4P＝88991，求F（P'）的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球、乒乓球、篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并将通过获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：
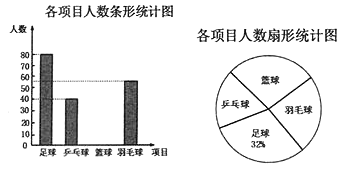
（1）这次活动一共调查了______名学生；
（2）补全条形统计图；
（3）选择篮球项目的人数在扇形统计图中，所占的百分比为______；
（4）若该学校有1500人，请你估计该学校选择足球项目的学生人数约是多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以A点为圆心，以相同的长为半径作弧，分别与射线AM，AN交于B，C两点，连接BC，再分别以B，C为圆心，以相同长（大于
BC）为半径作弧，两弧相交于点D，连接AD，BD，CD．则下列结论错误的是（ ）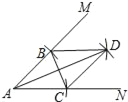
A. AD平分∠MAN B. AD垂直平分BC
C. ∠MBD=∠NCD D. 四边形ACDB一定是菱形
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线AB：y＝﹣
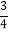x+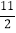
与直线AC：y＝
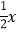+8交于点A，直线AB分别交x轴、y轴于B、E，直线AC分别交x轴、y轴于点C、D．（1）求点A的坐标；
（2）在y轴左侧作直线FG∥y轴，分别交直线AB、直线AC于点F、G，当FG＝3DE时，过点G作直线GH⊥y轴于点H，在直线GH上找一点P，使|PF﹣PO|的值最大，求出P点的坐标及|PF﹣PO|的最大值；
（3）将一个45°角的顶点Q放在x轴上，使其角的一边经过A点，另一边交直线AC于点R，当△AQR为等腰直角三角形时，请直接写出点R的坐标．
-
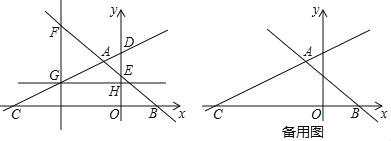
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P为边长为2的正方形ABCD的对角线BD上任一点，过点P作PE⊥BC于点E，PF⊥CD于点F，连接EF．给出以下4个结论：①AP＝EF；②AP⊥EF；③EF最短长度为
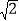；④若∠BAP＝30°时，则EF的长度为2．其中结论正确的有（ ）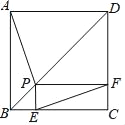
A. ①②③B. ①②④C. ②③④D. ①③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，BC=5，AC=12，M为斜边AB上一动点，过M作MD⊥AC，过M作ME⊥CB于点E，则线段DE的最小值为_______.
相关试题
