Question

【题目】如图，在Rt△ABC中，∠C=90°，BC=5，AC=12，M为斜边AB上一动点，过M作MD⊥AC，过M作ME⊥CB于点E，则线段DE的最小值为_______.

Answer 1

【答案】

【解析】由已知条件，易证四边形CDME是矩形，则DE=CM，由于无法直接求出DE的最小值，故可通过求CM的最小值进行解答；

由垂线段最短可知，当CM⊥AB时，CM取得最小值，在Rt△ABC中，由等面积法计算出CM的长度，问题即可解答.

如下图所示，连接CM.

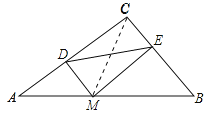
∵MD⊥AC，ME⊥CB，

∴∠MDC=∠MEC=90°.

∵∠ACB=90°，

∴四边形CDME是矩形，

∴DE=CM.

∵∠ACB=90°，BC=5，AC=12，

∴AB=.

当CM⊥AB时，CM最短，此时△ABC的面积=AB·CM=BC·AC=30，

∴CM的最小值=.

∴线段DE的最小值为.