【题目】计算:
(1)-23+![]() (2 018+3)0-
(2 018+3)0-![]() ; (2)992-69×71;
; (2)992-69×71;
(3) ![]() ÷(-3xy); (4)(-2+x)(-2-x);
÷(-3xy); (4)(-2+x)(-2-x);
(5)(a+b-c)(a-b+c); (6)(3x-2y+1)2.
参考答案:
【答案】(1)原式=-16![]() ;(2)原式=4 902;(3)原式=-
;(2)原式=4 902;(3)原式=-![]() x2y2-
x2y2-![]() xy+1;(4)原式=4-x2;(5)原式=a2-b2-c2+2bc;(6)原式=9x2+4y2-12xy+6x-4y+1.
xy+1;(4)原式=4-x2;(5)原式=a2-b2-c2+2bc;(6)原式=9x2+4y2-12xy+6x-4y+1.
【解析】试题分析:(1)第一项表示23的相反数,第二项非零数的零次幂等于1,第三项负整数指数幂等于这个数正整数指数幂的倒数;(2)把69×71改写成(70-1)×(70+1)计算;(3)按照多项式除以单项式的法则计算;(4)利用平方差公式计算;(5)把原式改写成[a+(b+c)][ a-(b+c)], 先根据平方差公式计算,再用完全平方公式计算;(6)把原式改写成[(3x-2y)+1]2,根据完全平方公式计算.
解:(1)原式=-8+![]() -9=-17+
-9=-17+![]() =-16
=-16![]() .
.
(2)原式=(100-1)2-(70-1)×(70+1)=10 000-200+1-4 900+1=4 902.
(3)原式=-![]() x2y2-
x2y2-![]() xy+1.
xy+1.
(4)原式=(-2)2-x2=4-x2.
(5)原式=a2-![]() =a2-b2-c2+2bc.
=a2-b2-c2+2bc.
(6)原式=[(3x-2y)+1]2
=(3x-2y)2+2(3x-2y)+1
=9x2+4y2-12xy+6x-4y+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次“寻宝”游戏中,已知寻宝图上两标志点A和点B的坐标分别为(-3,0),(5,0),“宝藏”分别埋在C(3,4)和D(-2,3)两点.
(1)请建立平面直角坐标系,并确定“宝藏”的位置;
(2)计算四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水—清洗—灌水”中水量y(m3)与时间t(min)之间的函数图象.
(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数表达式;
(2)问排水、清洗、灌水各花多少时间?

-
科目: 来源: 题型:
查看答案和解析>>【题目】用分解因式法解方程:
(1)4x2-12x=0;(2)25x2-9=0;(3)3y2-5y=0;(4)
 ;
;(5)4(x+3)2-(x-2)2=0 ;(6)4y2+12y+9=0;(7)
 ;
;(8)4(x-3) 2-x(x-3)=0;(9)(x-3)2-2(x-3)+1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的三个顶点的坐标分别为
的三个顶点的坐标分别为 、
、 、
、 .
.(1)请直接写出点
 关于
关于 轴对称的点的坐标;
轴对称的点的坐标;(2)将
 绕坐标原点
绕坐标原点 逆时针旋转90°.画出图形,直接写出点
逆时针旋转90°.画出图形,直接写出点 的对应点的坐标;
的对应点的坐标;(3)请直接写出:以
 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
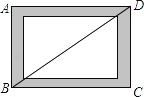
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图
 所示,点
所示,点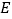 为矩形
为矩形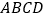 边
边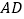 的中点,在矩形
的中点,在矩形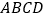 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员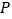 从点
从点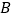 出发,沿着
出发,沿着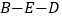 的路线匀速行进,到达点
的路线匀速行进,到达点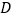 .设运动员
.设运动员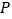 的运动时间为
的运动时间为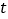 ,到监测点的距离为
,到监测点的距离为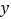 .现有
.现有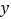 与
与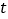 的函数关系的图象大致如图
的函数关系的图象大致如图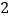 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).

A. 监测点
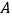 B. 监测点
B. 监测点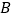 C. 监测点
C. 监测点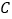 D. 监测点
D. 监测点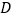
相关试题

