【题目】游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水—清洗—灌水”中水量y(m3)与时间t(min)之间的函数图象.
(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数表达式;
(2)问排水、清洗、灌水各花多少时间?

参考答案:
【答案】(1)答案见解析;(2) 答案见解析
【解析】解:(1)排水阶段:设解析式为:y=kt+b,
图象经过(0,1500),(25,1000),则:
![]()
解得:k=-20,b=1500,
故排水阶段解析式为:y=-20t+1500;
清洗阶段:y=0,
灌水阶段:设解析式为:y=at+c,
图象经过(195,1000),(95,0),则:
![]()
解得:a=10,c=-950,
灌水阶段解析式为:y=10t-950;
(2)∵排水阶段解析式为:y=-20t+1500;
∴y=0时,0=-20t+1500,
解得:t=75,
则排水时间为75分钟,
清洗时间为:95-75=20(分钟),
∵根据图象可以得出游泳池蓄水量为1500(m3),
∴1500=10t-950,
解得:t=245,
故灌水所用时间为:245-95=150(分钟).
答:排水时间为75分钟;清洗时间20分钟;灌水所用时间150分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样的题目:把方程
 x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:
x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.现在把上面的题目改编成下面的两个小题,请回答问题:(1)下面式子中是方程
 x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)
x2-x=2化为一元二次方程的一般形式的是________.(只填写序号)①
 x2-x-2=0,②-
x2-x-2=0,②-  x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤
x2+x+2=0,③x2-2x=4,④-x2+2x+4=0,⑤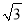 x2-2
x2-2 x-4
x-4 =0.
=0.(2)方程
 x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系?
x2-x=2化为一元二次方程的一般形式后,它的二次项系数,一次项系数和常数项之间具有什么关系? -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学实验课上,李静同学剪了两张直角三角形纸片,进行如下的操作:
操作一:如图1,将Rt△ABC纸片沿某条直线折叠,使斜边两个端点A与B重合,折痕为DE.
(1)如果AC=5cm,BC=7cm,可得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=1:2,可得∠B的度数为 ;
操作二:如图2,李静拿出另一张Rt△ABC纸片,将直角边AC沿直线CD折叠,使点A与点E重合,若AB=10cm,BC=8cm,请求出BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次“寻宝”游戏中,已知寻宝图上两标志点A和点B的坐标分别为(-3,0),(5,0),“宝藏”分别埋在C(3,4)和D(-2,3)两点.
(1)请建立平面直角坐标系,并确定“宝藏”的位置;
(2)计算四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用分解因式法解方程:
(1)4x2-12x=0;(2)25x2-9=0;(3)3y2-5y=0;(4)
 ;
;(5)4(x+3)2-(x-2)2=0 ;(6)4y2+12y+9=0;(7)
 ;
;(8)4(x-3) 2-x(x-3)=0;(9)(x-3)2-2(x-3)+1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-23+
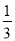 (2 018+3)0-
(2 018+3)0- ; (2)992-69×71;
; (2)992-69×71;(3)
 ÷(-3xy); (4)(-2+x)(-2-x);
÷(-3xy); (4)(-2+x)(-2-x);(5)(a+b-c)(a-b+c); (6)(3x-2y+1)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的三个顶点的坐标分别为
的三个顶点的坐标分别为 、
、 、
、 .
.(1)请直接写出点
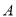 关于
关于 轴对称的点的坐标;
轴对称的点的坐标;(2)将
 绕坐标原点
绕坐标原点 逆时针旋转90°.画出图形,直接写出点
逆时针旋转90°.画出图形,直接写出点 的对应点的坐标;
的对应点的坐标;(3)请直接写出:以
 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点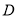 的坐标.
的坐标.
相关试题

