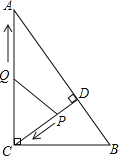
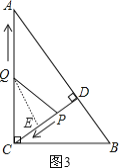
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得
S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,则说明理由.
(3)是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.
参考答案:
【答案】(1)4.8;(2)t=![]() 或t=3;(3)t=2.4秒或
或t=3;(3)t=2.4秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
试题分析:(1)根据勾股定理得出AB的长度,利用等面积法求出线段CD的长度;(2)过点P⊥PH⊥AC,根据题意得出DP=t,CQ=t,则CP=4.8-t,根据△CHP∽△BCA得出PH的长度,然后求出△CPQ与t的函数关系式,然后根据三角形的面积之比得出答案;(3)本题分CQ=CP、PQ=PC以及QC=QP三种情况得出答案.
试题解析:(1)如图1, ∵∠ACB=90°,AC=8,BC=6,
∴AB=10. ∵CD⊥AB,
∴S△ABC=![]() BCAC=
BCAC=![]() ABCD.
ABCD.
∴CD=![]() =
=![]() =4.8.
=4.8.
∴线段CD的长为4.8.
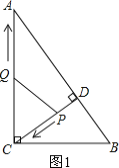
(2)过点P作PH⊥AC,垂足为H,如图2所示.
由题可知DP=t,CQ=t. 则CP=4.8﹣t.
∵∠ACB=∠CDB=90°,
∴∠HCP=90°﹣∠DCB=∠B.
∵PH⊥AC,
∴∠CHP=90°.
∴∠CHP=∠ACB.
∴△CHP∽△BCA.
∴![]() . ∴
. ∴![]() .
.
∴PH=![]() ﹣
﹣![]() t.
t.
∴S△CPQ=![]() CQPH=
CQPH=![]() t(
t(![]() ﹣
﹣![]() t)=﹣
t)=﹣![]() t2+
t2+![]() t.
t.
存在某一时刻t,使得S△CPQ:S△ABC=9:100.
∵S△ABC=![]() ×6×8=24,
×6×8=24,
且S△CPQ:S△ABC=9:100,
∴(﹣![]() t2+
t2+![]() t):24=9:100.
t):24=9:100.
整理得:5t2﹣24t+27=0.
即(5t﹣9)(t﹣3)=0.
解得:t=![]() 或t=3.
或t=3.
∵0≤t≤4.8,
∴当t=![]() 秒或t=3秒时,S△CPQ:S△ABC=9:100.
秒或t=3秒时,S△CPQ:S△ABC=9:100.
(3)存在
①若CQ=CP,如图1,则t=4.8﹣t.
解得:t=2.4
②若PQ=PC,如图2所示.
∵PQ=PC,PH⊥QC,
∴QH=CH=![]() QC=
QC=![]() .
.
∵△CHP∽△BCA.
∴![]() .
.
∴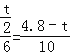 .
.
解得;t=![]() .
.
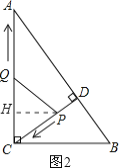
③若QC=QP,过点Q作QE⊥CP,垂足为E,如图3所示
同理可得:t=![]() .
.
综上所述:当t为2.4秒或![]() 秒或
秒或![]() 秒时,△CPQ为等腰三角形.
秒时,△CPQ为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a3+a2=a5 B. a6÷a3=a2 C. (a2)3=a8 D. a2·a3=a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在1、﹣1、3、﹣2这四个数中,互为相反数的是( )
A.1与﹣1
B.1与﹣2
C.3与﹣2
D.﹣1与﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,能用提公因式分解因式的是( )
A. x2-y B. x2+2x C. x2+y2 D. x2-xy+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:

(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD,
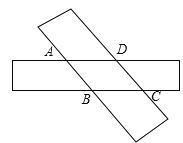
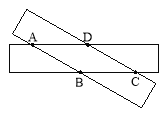 (1试判断四边形ABCD的形状,并说明理由
(1试判断四边形ABCD的形状,并说明理由(2)若∠BAD=30°,求重叠部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个扇形满足弧长的比等于它们半径的比,则这称这两个扇形相似。如图,如果扇形AOB与扇形
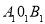 是相似扇形,且半径
是相似扇形,且半径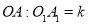 (
(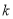 为不等于0的常数)那么下面四个结论:①∠AOB=∠
为不等于0的常数)那么下面四个结论:①∠AOB=∠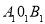 ;②△AOB∽△
;②△AOB∽△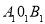 ;③
;③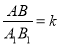 ;④扇形AOB与扇形
;④扇形AOB与扇形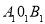 的面积之比为
的面积之比为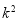 。成立的个数为:( )
。成立的个数为:( )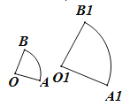
A、1个 B、2个 C、3个 D、4个
相关试题

