【题目】如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是cm2 . 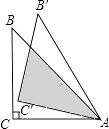
参考答案:
【答案】6 ![]()
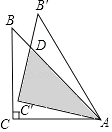
【解析】解:AB与C′B′相交于点D,如图,
∵等腰Rt△ABC中,∠C=90°,BC=6cm,
∴AC=BC=6cm,∠CAB=45°,
∵△ABC绕点A顺时针旋转15°后得到△AB′C′,
∴∠CAB=45°,CA=C′A=15°,
∴∠C′AD=30°,
在Rt△AC′D中,C′D= ![]() AC′=
AC′= ![]() ×6=2
×6=2 ![]() ,
,
∴阴影部分的面积= ![]() ×6×2
×6×2 ![]() =6
=6 ![]() .
.
所以答案是6 ![]() .
.
【考点精析】本题主要考查了等腰直角三角形和旋转的性质的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=AC,∠C=90°,直角顶点C在x轴上,一锐角顶点B在y轴上.
(1)如图①若AD于垂直x轴,垂足为点D.点C坐标是(﹣1,0),点A的坐标是(﹣3,1),求点B的坐标.
(2)如图②,直角边BC在两坐标轴上滑动,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,请猜想BD与AE有怎样的数量关系,并证明你的猜想.
(3)如图③,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,请猜想OC,AF,OB之间有怎样的关系(直接写出结论,不需要证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作图的切线。
已知:P为圆O外一点。
求作:经过点P的圆O的切线。
小敏的作法如下:
①连接OP,作线段OP的垂直平分线MN交OP于点C;
②以点C为圆心,CO的长为半径作圆交圆O于A、B两点;
③作直线PA、PB,所以直线PA、PB就是所求作的切线。
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作图的切线。
已知:P为圆O外一点。
求作:经过点P的圆O的切线。
小敏的作法如下:
①连接OP,作线段OP的垂直平分线MN交OP于点C;
②以点C为圆心,CO的长为半径作圆交圆O于A、B两点;
③作直线PA、PB,所以直线PA、PB就是所求作的切线。
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知一次函数y=﹣
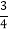 x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )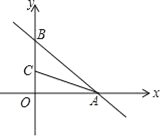
A. (0,3) B. (0,
 ) C. (0,
) C. (0, ) D. (0,
) D. (0, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】设计调查问卷时,下列提问是否合适?如果不合适的话应该怎样改进?
(1)你上学时使用的交通工具是
 .汽车
.汽车 .摩托车
.摩托车 .步行
.步行 .其他
.其他(2)你对老师的教学满意吗?
 .比较满意
.比较满意 .满意
.满意 .非常满意.
.非常满意.
相关试题

