搜索
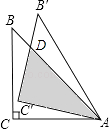
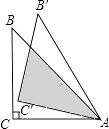
【题目】如图，等腰Rt△ABC中，∠C=90°，BC=6cm，将△ABC绕点A顺时针旋转15°后得到△AB′C′，则图中阴影部分的面积是cm2 ． 
参考答案：
【答案】6 
【解析】解：AB与C′B′相交于点D，如图，
∵等腰Rt△ABC中，∠C=90°，BC=6cm，
∴AC=BC=6cm，∠CAB=45°，
∵△ABC绕点A顺时针旋转15°后得到△AB′C′，
∴∠CAB=45°，CA=C′A=15°，
∴∠C′AD=30°，
在Rt△AC′D中，C′D= 
AC′= ×6=2 ，
∴阴影部分的面积= 
×6×2 =6 ．
所以答案是6 ．
【考点精析】本题主要考查了等腰直角三角形和旋转的性质的相关知识点，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O上有两点A与P，且OA⊥OP，若A点固定不动，P点在圆上匀速运动一周，那么弦AP的长度d与时间t的函数关系的图象可能是（ ）
A.①
B.③
C.①或③
D.②或④ -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学开展“八荣八耻”演讲比赛活动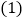，九
、九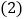
班根据初赛成绩各选出
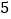名选手参加复赛，两个班各选出的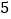名选手的复赛成绩（满分为
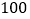分）如下图所示：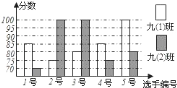
（1）根据上图填写下表：
平均分（分）
中位数（分）
众数（分）
九
班
九
班
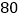
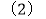结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好？（3）如果在每班参加复赛的选手中分别选出
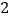人参加决赛，你认为哪个班的实力更强一些，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某九年级制学校围绕“每天30分钟的大课间，你最喜欢的体育活动项目是什么？（只写一项）”的问题，对在校学生进行随机抽样调查，从而得到一组数据．图1是根据这组数据绘制的条形统计图，请结合统计图回答下列问题：
（1）该校对多少学生进行了抽样调查？
（2）本次抽样调查中，最喜欢篮球活动的有多少？占被调查人数的百分比是多少？
（3）若该校九年级共有200名学生，图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图，请你估计全校学生中最喜欢跳绳活动的人数约为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，BC=AC，∠C=90°，直角顶点C在x轴上，一锐角顶点B在y轴上．
（1）如图①若AD于垂直x轴，垂足为点D．点C坐标是（﹣1，0），点A的坐标是（﹣3，1），求点B的坐标．
（2）如图②，直角边BC在两坐标轴上滑动，若y轴恰好平分∠ABC，AC与y轴交于点D，过点A作AE⊥y轴于E，请猜想BD与AE有怎样的数量关系，并证明你的猜想．
（3）如图③，直角边BC在两坐标轴上滑动，使点A在第四象限内，过A点作AF⊥y轴于F，在滑动的过程中，请猜想OC，AF，OB之间有怎样的关系（直接写出结论，不需要证明）
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
在学习《圆》这一章时，老师给同学们布置了一道尺规作图题：
尺规作图：过圆外一点作图的切线。
已知：P为圆O外一点。
求作：经过点P的圆O的切线。
小敏的作法如下：
①连接OP，作线段OP的垂直平分线MN交OP于点C；
②以点C为圆心，CO的长为半径作圆交圆O于A、B两点；
③作直线PA、PB，所以直线PA、PB就是所求作的切线。
老师认为小敏的作法正确．
请回答：连接OA，OB后，可证∠OAP=∠OBP=90°，其依据是；由此可证明直线PA，PB都是⊙O的切线，其依据是 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰Rt△ABC中，∠C=90°，BC=6cm，将△ABC绕点A顺时针旋转15°后得到△AB′C′，则图中阴影部分的面积是cm2 ．
相关试题
