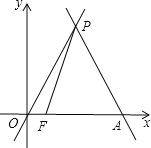
【题目】已知:如图,直线y=﹣![]() x+4
x+4![]() 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y=![]() x交于点P.
x交于点P.
(1)求点P的坐标.
(2)动点F从原点O出发,以每秒1个单位的速度在线段OA上向点A作匀速运动,连接PF,设运动时间为t秒,△PFA的面积为S,求出S关于t的函数关系式.
(3)若点M是y轴上任意一点,点N是坐标平面内任意一点,若以O、M、N、P为顶点的四边形是菱形,请直接写出点N的坐标.
参考答案:
【答案】(1)P点坐标(2,2![]() );(2)S=4
);(2)S=4![]() ﹣
﹣![]() t(0≤t<4);(3)N点坐标为N1(2,2
t(0≤t<4);(3)N点坐标为N1(2,2![]() ﹣4),N2(2,2
﹣4),N2(2,2![]() +4),N3(﹣2,2
+4),N3(﹣2,2![]() ),N4(2,
),N4(2,![]() ).
).
【解析】
(1)联立两直线的解析式求出x、y的值即可得出P点坐标;
(2)先求出A点坐标,再根据三角形的面积公式即可得出结论;
(3)分OP为菱形的边与对角线两种情况进行讨论.
解:(1)∵由已知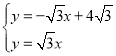 ,
,
解得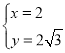 ,
,
∴P点坐标(2,2![]() );
);
(2)∵直线y=﹣![]() x+4
x+4![]() 中,当y=0时,x=4,
中,当y=0时,x=4,
∴OA=4,
∴S=![]() (OA﹣t)×2
(OA﹣t)×2![]() =
=![]() (4﹣t)×2
(4﹣t)×2![]() =4
=4![]() ﹣
﹣![]() t(0≤t<4);
t(0≤t<4);
(3)如图,当OP为平行四边形的边时,
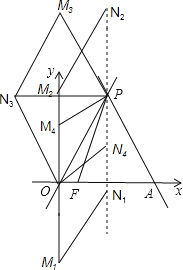
∵P(2,2![]() ),
),
∴OP=![]() =4,
=4,
∴N1(2,2![]() ﹣4),N2(2,2
﹣4),N2(2,2![]() +4),N3(﹣2,2
+4),N3(﹣2,2![]() );
);
当OP为对角线时,设M(0,a),
则MP=a,即22+(2![]() ﹣a)2=a2,解得a=
﹣a)2=a2,解得a=![]() ,
,
∴N点的纵坐标=2![]() ﹣
﹣![]() =
=![]() ,
,
∴N4(2,![]() ).
).
综上所示,N点坐标为N1(2,2![]() ﹣4),N2(2,2
﹣4),N2(2,2![]() +4),N3(﹣2,2
+4),N3(﹣2,2![]() ),N4(2,
),N4(2,![]() ).
).
-
科目: 来源: 题型:
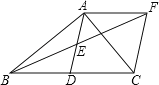
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知G、H分别是□ABCD对边AD、BC上的点,直线GH分别交BA和DC的延长线于点E、F.
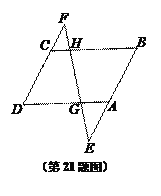
(1)当
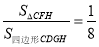 时,求
时,求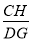 的值;
的值;(2)联结BD交EF于点M,求证:MG·ME=MF·MH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为i=1:
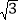 的斜坡CD前进2
的斜坡CD前进2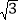 米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(精确到0.1).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
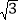 ≈1.73.)
≈1.73.)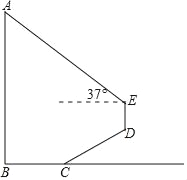
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(-1,0),点B在直线
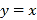 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )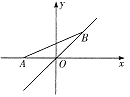
A. (0,0) B. (
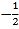 ,
,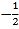 ) C. (
) C. (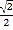 ,
,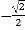 ) D. (
) D. (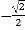 ,
,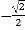 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在锐角△ABC中,CE⊥AB于点E,点D在边AC上,联结BD交CE于点F,且EF·FC=FB·DF.
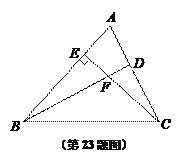
(1)求证:BD⊥AC;
(2)联结AF,求证:AF·BE=BC·EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若|a|=-b,|b|=b,则a=b=0;②若-a不是正数,则a为非负数;③|-a
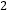 |=(-a)
|=(-a)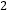 ; ④若
; ④若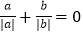 ,则
,则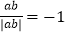 ; ⑤若a+b=0,则a3+b3=0; ⑥若|a|>b,则a2>b2;其中正确的结论有( )
; ⑤若a+b=0,则a3+b3=0; ⑥若|a|>b,则a2>b2;其中正确的结论有( )A.2个B.3个C.4个D.5个
相关试题

