【题目】如图,已知G、H分别是□ABCD对边AD、BC上的点,直线GH分别交BA和DC的延长线于点E、F.
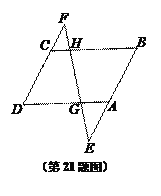
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)联结BD交EF于点M,求证:MG·ME=MF·MH.
参考答案:
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)由![]() ,得
,得![]() .由于△CFH∽△DFG,由相似三角形面积的比等于相似比的平方,即可求得结果;
.由于△CFH∽△DFG,由相似三角形面积的比等于相似比的平方,即可求得结果;
(2)根据平行四边形的性质得出AB∥CD,AD//BC,由平行线分线段成比例得出比例式,即可得出答案.
试题解析:(1)∵![]() ,
,
∴![]() .
.
∵ □ABCD中,AD//BC,
∴ △CFH∽△DFG ,
∴![]() (
(![]() )2
)2![]() ,
,
∴![]() =
=![]() .
.
(2)证明:∵ □ABCD中,AD//BC,
∴![]() ,
,
∵ □ABCD中,AB//CD,
∴![]() ,
,
∴![]() .
.
∴MG·ME=MF·MH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】包装厂有42名工人,每人平均每天可以生产圆形铁片120片或长方形铁片80片.为了每天生产的产品刚好制成一个密封的圆桶,应该分配多少名工人生产圆形铁片,多少名工人生产长方形铁片?设应分配x名工人生产长方形铁片,(42-x)名工人生产圆形铁片,则下列所列方程正确的是( )
A. 120x=2×80(42-x) B. 80x=120(42-x)
C. 2×80x=120(42-x) D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与x轴、y轴分别交于点A,B,点C是线段AB上一点,四边形OADC是菱形,求OD的长.
与x轴、y轴分别交于点A,B,点C是线段AB上一点,四边形OADC是菱形,求OD的长. 
-
科目: 来源: 题型:
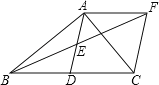
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为i=1:
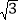 的斜坡CD前进2
的斜坡CD前进2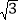 米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(精确到0.1).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
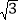 ≈1.73.)
≈1.73.)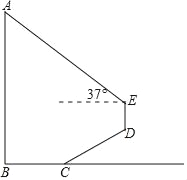
-
科目: 来源: 题型:
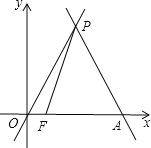
查看答案和解析>>【题目】已知:如图,直线y=﹣
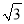 x+4
x+4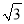 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y=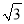 x交于点P.
x交于点P.(1)求点P的坐标.
(2)动点F从原点O出发,以每秒1个单位的速度在线段OA上向点A作匀速运动,连接PF,设运动时间为t秒,△PFA的面积为S,求出S关于t的函数关系式.
(3)若点M是y轴上任意一点,点N是坐标平面内任意一点,若以O、M、N、P为顶点的四边形是菱形,请直接写出点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(-1,0),点B在直线
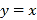 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )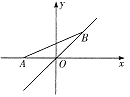
A. (0,0) B. (
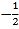 ,
,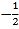 ) C. (
) C. (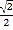 ,
,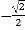 ) D. (
) D. (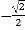 ,
,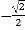 )
)
相关试题

