【题目】已知:△ABC中,AE平分∠BAC。
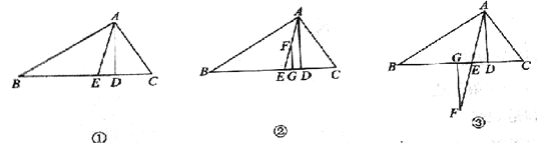
(1)如图①AD⊥BC于D,若∠C =70°,∠B =30°,求∠DAE的度数
(2)如图②所示,在△ABC中AD⊥BC,AE平分∠BAC,F是AE上的任意一点,过F作FG⊥BC于G,且∠B=40°,∠C=80°,求∠EFG的度数;
(3)在(2)的条件下,若F点在AE的延长线上(如图③),其他条件不变,则∠EFG的角度大小发生改变吗?说明理由.
参考答案:
【答案】(1)20°;(2)20°;(3)∠EFG的度数大小不发生改变.
【解析】试题分析:(1)由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=![]() ∠BAC,故∠EAD=∠EAC-∠DAC;
∠BAC,故∠EAD=∠EAC-∠DAC;
(2)推出AD∥FG,根据平行线性质得出∠EFG=∠DAE,代入即可.
(3)推出AD∥FG,根据平行线性质得出∠EFG=∠DAE,代入即可.
试题解析:(1)∵在△ABC中,AE是∠BAC的平分线,且∠B=30°,∠C=70°,
∴∠BAE=∠EAC=![]() (180°-∠B-∠C)=
(180°-∠B-∠C)=![]() (180°-30°-70°)=40°.
(180°-30°-70°)=40°.
在△ACD中,∠ADC=90°,∠C=70°,
∴∠DAC=90°-70°=20°,
∠DAE=∠EAC-∠DAC=40°-20°=20°.
(2)∵∠B=40°,∠C=80°,
∴∠DAE=![]() ×80°-
×80°-![]() ×40°=20°,
×40°=20°,
∵AD⊥BC,FG⊥BC,
∴∠ADE=∠FGE=90°,
∴AD∥FG,
∴∠EFG=∠DAE=20°;
(3)∠EFG的度数大小不发生改变,
理由是:∵AD⊥BC,FG⊥BC,
∴∠ADE=∠FGE=90°,
∴AD∥FG,
∴∠EFG=∠DAE=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=6.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数据2,2,3,2,5,2,10,2,5,2,3 ①众数是2 ②众数与中位数的数值不等 ③中位数与平均数相等 ④平均数与众数的数值相等.其中正确的结论有 ( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A.12
B.9
C.12或9
D.9或7 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知4m=a,8n=b,用含a,b的式子表示下列代数式: ①求:22m+3n的值,
②求:24m﹣6n的值;
(2)已知2×8x×16=223,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式运算正确的是( )
A.a3+a2=2a5
B.a3﹣a2=a
C.(a3)2=a5
D.a6÷a3=a3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c满足(a﹣7.5)2+
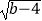 +|c﹣8.5|=0.求:
+|c﹣8.5|=0.求:
(1)a、b、c的值;
(2)求以a、b、c为边构成的三角形面积.
相关试题

