【题目】如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=6.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= . 
参考答案:
【答案】4 ![]()
【解析】解:∵DC=3DE=6,
∴DE=2,CE=4,
由翻折变换得,PE=CE,FP=FC,∠EPF=∠C=90°,∠CFE=∠PFE,
所以,在Rt△DPE中,∠DPE=30°,
所以,∠DPF=∠EPF+∠DPE=90°+30°=120°,
∵矩形对边AD∥BC,
∴∠CFP=180°﹣∠DPF=180°﹣120°=60°,
∴∠CFE= ![]() ∠CFP=
∠CFP= ![]() ×60°=30°,
×60°=30°,
∴EF=2CE=2×4=8,
在Rt△CEF中,根据勾股定理得,FC= ![]() =
= ![]() =4
=4 ![]() .
.
所以答案是:4 ![]() .
.
【考点精析】根据题目的已知条件,利用矩形的性质和翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于
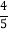 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3b3=(ab)3
B.a2a3=a6
C.a6÷a3=a2
D.(a2)3=a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线________.
(1)它的理由如下:(如图1)
∵b⊥a,c⊥a,∴∠1=∠2=90°,
∴b∥c________
(2)如图2是木工师傅使用角尺画平行线,有什么道理?________.
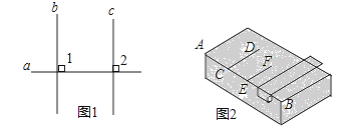
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数据2,2,3,2,5,2,10,2,5,2,3 ①众数是2 ②众数与中位数的数值不等 ③中位数与平均数相等 ④平均数与众数的数值相等.其中正确的结论有 ( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A.12
B.9
C.12或9
D.9或7 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC中,AE平分∠BAC。
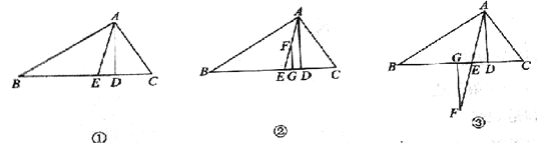
(1)如图①AD⊥BC于D,若∠C =70°,∠B =30°,求∠DAE的度数
(2)如图②所示,在△ABC中AD⊥BC,AE平分∠BAC,F是AE上的任意一点,过F作FG⊥BC于G,且∠B=40°,∠C=80°,求∠EFG的度数;
(3)在(2)的条件下,若F点在AE的延长线上(如图③),其他条件不变,则∠EFG的角度大小发生改变吗?说明理由.
相关试题

