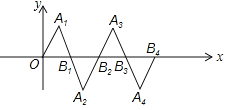
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A.(4n﹣1,![]() ) B.(2n﹣1,
) B.(2n﹣1,![]() ) C.(4n+1,
) C.(4n+1,![]() ) D.(2n+1,
) D.(2n+1,![]() )
)
参考答案:
【答案】C.
【解析】
试题分析:∵△OA1B1是边长为2的等边三角形,∴A1的坐标为(1,![]() ),B1的坐标为(2,0),∵△B2A2B1与△OA1B1关于点B1成中心对称,∴点A2与点A1关于点B1成中心对称,∵2×2﹣1=3,2×0
),B1的坐标为(2,0),∵△B2A2B1与△OA1B1关于点B1成中心对称,∴点A2与点A1关于点B1成中心对称,∵2×2﹣1=3,2×0![]() =
=![]() ,∴点A2的坐标是(3,
,∴点A2的坐标是(3,![]() ),
),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,∴点A3与点A2关于点B2成中心对称,∵2×4﹣3=5,2×0﹣(![]() )=
)=![]() ,∴点A3的坐标是(5,
,∴点A3的坐标是(5,![]() ),
),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,∴点A4与点A3关于点B3成中心对称,∵2×6﹣5=7,2×0![]() =
=![]() ,∴点A4的坐标是(7,
,∴点A4的坐标是(7,![]() ),
),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,
∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是![]() ,当n为偶数时,An的纵坐标是
,当n为偶数时,An的纵坐标是![]() ,∴顶点A2n+1的纵坐标是
,∴顶点A2n+1的纵坐标是![]() ,
,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,![]() ).故选C.
).故选C.
-
科目: 来源: 题型:
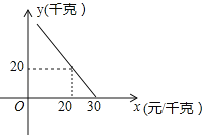
查看答案和解析>>【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别是3和7,则它的周长为( )
A.17
B.15
C.13
D.13或17 -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,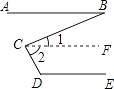
证明:过点C作CF∥AB.
∵AB∥CF(已知),
∴∠B=().
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ()
∴∠2+=180° ()
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° (). -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正比例函数的图像经过A(3,-6),B(m,-4)两点,则m的值为()
A.2B.8C.-2D.-8
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示0.0000907= .
-
科目: 来源: 题型:
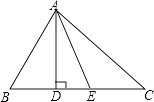
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠AEC的度数.
相关试题

