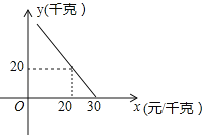
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
参考答案:
【答案】(1)![]() ;(2)当销售单价为20元/千克时,每天可获得最大利润200元.
;(2)当销售单价为20元/千克时,每天可获得最大利润200元.
【解析】
试题分析:(1)由图象过点(20,20)和(30,0),利用待定系数法求直线解析式;
(2)每天利润=每千克的利润×销售量.由此列出表达式,然后用函数性质解答.
试题解析:(1)设![]() ,由图象可知,
,由图象可知,![]() ,解之,得:
,解之,得:![]() ,∴
,∴![]() ;
;
(2)p=(x﹣10)y=(x﹣10)(﹣2x+60)=![]() =
=![]() ,∵a=﹣2<0,∴p有最大值,当x=20时,p最大值=200.
,∵a=﹣2<0,∴p有最大值,当x=20时,p最大值=200.
即当销售单价为20元/千克时,每天可获得最大利润200元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼.小丽在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,下列说法不正确的是( )
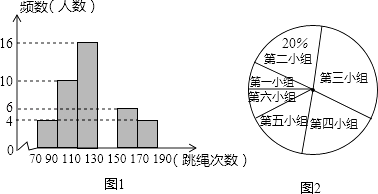
A.第四小组有10人
B.第五小组对应圆心角的度数为45°
C.本次抽样调查的样本容量为50
D.该校“一分钟跳绳”成绩优秀的人数约为480人 -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:
如图1,需要在A,B两地和公路l之间修地下管道,请你设计一种最节省材料的修建方案.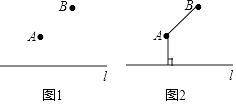
小军同学的作法如下:
①连接AB;
②过点A作AC⊥直线l于点C;
则折线段B﹣A﹣C为所求.
老师说:小军同学的方案是正确的.
请回答:该方案最节省材料的依据是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合,OD与BC交于点E,则点D的坐标是( )
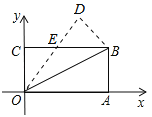
A.(4,8) B.(5,8) C.(
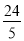 ,
,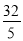 ) D.(
) D.(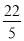 ,
,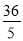 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边长分别是3和7,则它的周长为( )
A.17
B.15
C.13
D.13或17 -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,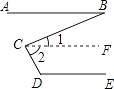
证明:过点C作CF∥AB.
∵AB∥CF(已知),
∴∠B=().
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ()
∴∠2+=180° ()
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° (). -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
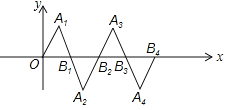
A.(4n﹣1,
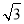 ) B.(2n﹣1,
) B.(2n﹣1,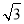 ) C.(4n+1,
) C.(4n+1,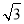 ) D.(2n+1,
) D.(2n+1,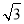 )
)
相关试题

