【题目】(1)如图,已知点C在线段AB上,AC=6cm,且BC=4cm,M、N分别是AC、BC的中点,求线段MN的长度;
![]()
(2)在(1)题中,如果![]() 其他条件不变,你能猜出MN的长度吗?请你用一句简洁的话表达你发现的规律;
其他条件不变,你能猜出MN的长度吗?请你用一句简洁的话表达你发现的规律;
(3)对于(1)题,当点C在BA的延长线上时,且AB=![]() 其他条件不变,求MN的长度.
其他条件不变,求MN的长度.
参考答案:
【答案】(1)5cm;(2)见解析;(3) ![]() .
.
【解析】
(1)根据线段中点的性质,可得MC、NC的长,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得MC、NC的长,根据线段的和差,可得答案;(3) 根据线段中点的性质,可得MC、NC的长,根据BC=AB+AC,可得MN=![]() .
.
(1)解:因为M,N分别是AC,BC的中点所以,
MC=![]() AC=
AC=![]() ×6=3cm,
×6=3cm,
NC=![]() BC=
BC=![]() ×4=2cm,
×4=2cm,
所以,MN=MC+NC=3+2=5(cm);
(2)解:由(1)知MC=![]() a,NC=
a,NC=![]() b,
b,
所以,MN=MC+NC=![]() a+
a+![]() b=
b=![]() (a+b).
(a+b).
规律:直线上相邻两线段中点间的距离为两线段长度和的一半.
(3) 当点C在线段BA的延长线时,如图:![]()
因为M,N分别是AC,BC的中点所以,
CM=![]() AC
AC
CN=![]() BC
BC
∴MN=CN-CM=![]() ,
,
∵BC=AB+AC,AB=m,
∴MN=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
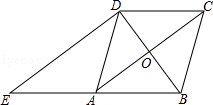
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】有20箱橘子,以每箱25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)20箱橘子中,最重的一箱比最轻的一箱多重多少干克?
(2)与标准重量比较,20箱橘子总计超过或不足多少千克?
(3)若橘子每千克售价2.5元,则出售这20箱橘子可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,
 ),B(﹣1,2)是一次函数y=kx+b与反比例函数
),B(﹣1,2)是一次函数y=kx+b与反比例函数 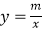 (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D. 
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是Rt△ABC的外接圆,AC是⊙O的直径,弦BD=BA,AB=12,BC=5,BE⊥DC,交DC的延长线于点E.
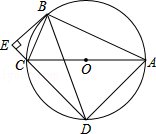
(1)求证:△ABC∽△DEB;
(2)求证:BE是⊙O的切线;
(3)求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答下列问题.
已知平面内两点 M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算: MN=
 .
.例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=
 =
= .
.特别地,如果两点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
(1)已知 A(1,2)、B(﹣2,﹣3),试求 A、B 两点间的距离;
(2)已知 A、B 在平行于 x 轴的同一条直线上,点 A 的横坐标为 5,点 B 的横坐标为﹣1,
试求 A、B 两 点间的距离;
(3)已知△ABC 的顶点坐标分别为 A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC 的形状 吗?请说明理由.
相关试题

