【题目】如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1) 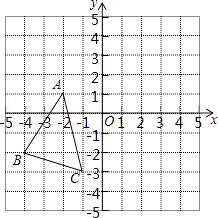
(1)A′、B′两点的坐标分别为A′、B′;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.
参考答案:
【答案】
(1)(3,5);(1,2)
(2)
解:△A′B′C′如图所示;
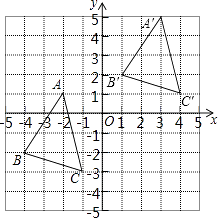
(3)
解:
S△A′B′C′=4×3﹣ ![]() ×3×1﹣
×3×1﹣ ![]() ×3×2﹣
×3×2﹣ ![]() ×1×4
×1×4
=12﹣1.5﹣3﹣2
=5.5
【解析】解:(1)∵△A′B′C′是△ABC平移之后得到的图象,并且C(﹣1,﹣3)的对应点C′的坐标为(4,1),
∴平移前后对应点的横坐标加5,纵坐标加4,
∴△ABC先向右平移5个单位,再向上平移4个单位得到△A′B′C′,
∵A(﹣2,1),B(﹣4,﹣2),
∴A′(3,5)、B′(1,2);
故答案为(3,5),(1,2)
(1)由点C(﹣1,﹣3)与点C′(4,1)是对应点,得出平移规律为:向右平移5个单位,向上平移4个单位,按平移规律即可写出所求的点的坐标;(2)按平移规律作出A、B的对应点A′,B′,顺次连接A′、B′、C′,即可得到△A′B′C′;(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据1,2,4,5,3的中位数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.

(1)直接写出图中∠AOC的对顶角: , ∠EOB的邻补角:
(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=12cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB,AC,AD于E,F,H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).
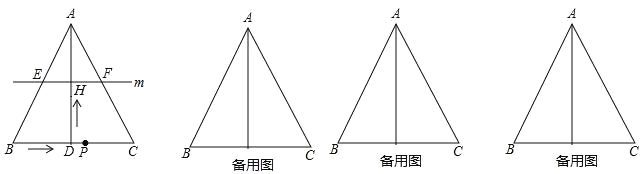
(1)连接DE、DF,当t为何值时,四边形AEDF为菱形?
(2)连接PE、PF,在整个运动过程中,△PEF的面积是否存在最大值?若存在,试求当△PEF的面积最大时,线段BP的长.
(3)是否存在某一时刻t,使点F在线段EP的中垂线上?若存在,请求出此时刻t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD= .
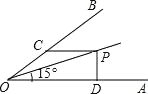
-
科目: 来源: 题型:
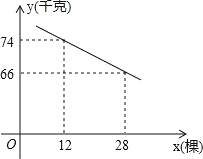
查看答案和解析>>【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出﹣a2b的同类项_____(只要求写一个).
相关试题

