【题目】在△ABC中,∠ABC=90°.
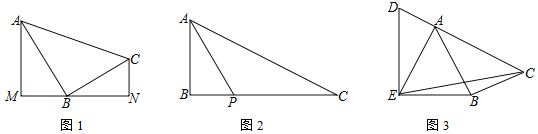
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=![]() ,求tanC的值;
,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=![]() ,
,![]() ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)利用同角的余角相等判断出∠BAM=∠CBN,即可得出结论;
(2)如图,过点P作PF⊥AP交AC于F,先判断出△ABP∽△PQF,得出![]() ,再判断出△ABP∽△CQF,得出CQ=2a,进而建立方程用b表示出a,即可得出结论;
,再判断出△ABP∽△CQF,得出CQ=2a,进而建立方程用b表示出a,即可得出结论;
(3)先判断出![]() ,再同(2)的方法,即可得出结论.
,再同(2)的方法,即可得出结论.
(1)∵AM⊥MN,CN⊥MN,
∴∠AMB=∠BNC=90°,
∴∠BAM+∠ABM=90°,
∵∠ABC=90°,
∴∠ABM+∠CBN=90°,
∴∠BAM=∠CBN,
∵∠AMB=∠NBC,
∴△ABM∽△BCN;
(2)如图,过点P作PF⊥AP交AC于F,
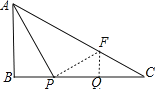
在Rt△AFP中,tan∠PAC=![]() ,
,
同(1)的方法得,△ABP∽△PQF,
∴![]() ,
,
设AB=![]() a,PQ=2a,BP=
a,PQ=2a,BP=![]() b,FQ=2b(a>0,b>0),
b,FQ=2b(a>0,b>0),
∵∠BAP=∠C,∠B=∠CQF=90°,
∴△ABP∽△CQF,
∴![]() ,∴CQ=
,∴CQ=![]() =2a,
=2a,
∵BC=BP+PQ+CQ=![]() b+2a+2a=4a+
b+2a+2a=4a+![]() b,
b,
∵∠BAP=∠C,∠B=∠B=90°,
∴△ABP∽△CBA,
∴![]() ,
,
∴BC=![]() ,
,
∴4a+![]() b=
b=![]() ,
,
∴a=![]() b,
b,
∴BC=4×![]() b+
b+![]() b=
b=![]() b,AB=
b,AB=![]() a=b,
a=b,
在Rt△ABC中,tanC=![]() ;
;
(3)在Rt△ABC中,sin∠BAC=![]() ,
,
如图,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,
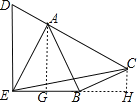
∵∠DEB=90°,
∴CH∥AG∥DE,
∴![]() ,
,
同(1)的方法得,△ABG∽△BCH,
∴![]() =
=![]() ,
,
设BG=4m,CH=3m,AG=4n,BH=3n,
∵AB=AE,AG⊥BE,
∴EG=BG=4m,
∴GH=BG+BH=4m+3n,
∴![]() ,
,
∴n=2m,
∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m,
在Rt△CEH中,tan∠BEC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“8字”的性质及应用:
(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
(2)图②中共有多少个“8字”?
(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=
 (∠A+∠C).
(∠A+∠C).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,m)在双曲线y=
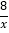 上且m<0,过点A作x轴的垂线,垂足为B.
上且m<0,过点A作x轴的垂线,垂足为B.(1)如图1,当a=﹣2时,P(t,0)是x轴上的动点,将点B绕点P顺时针旋转90°至点C,
①若t=1,直接写出点C的坐标;
②若双曲线y=
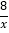 经过点C,求t的值.
经过点C,求t的值.(2)如图2,将图1中的双曲线y=
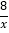 (x>0)沿y轴折叠得到双曲线y=﹣
(x>0)沿y轴折叠得到双曲线y=﹣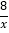 (x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣
(x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣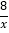 (x<0)上的点D(d,n)处,求m和n的数量关系.
(x<0)上的点D(d,n)处,求m和n的数量关系.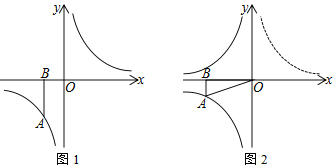
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:4(x+1)2-169=0;
(2)一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
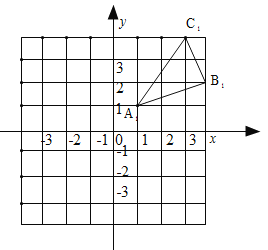
(1)请画出△ABC,并写出点A、B、C的坐标;
(2)求出△AOA1的面积.
-
科目: 来源: 题型:
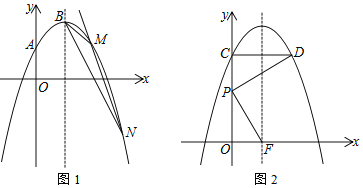
查看答案和解析>>【题目】抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的解析式;
(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
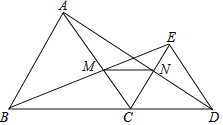
(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
相关试题

