搜索
【题目】（8分）如图，△A1B1C1是△ABC向右平移四个单位长度后得到的，且三个顶点的坐标分别为A1（1，1），B1（4，2），C1（3，4）．
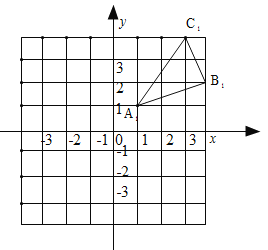
（1）请画出△ABC，并写出点A、B、C的坐标；
（2）求出△AOA1的面积．
参考答案：
【答案】（1）作图见试题解析，A（－3，1）， B（0，2），C（－1，4）；（2）2．
【解析】
试题（1）△A1B1C1是由△ABC向右平移4个单位得到的，故将△A1B1C1向左平移4个单位既是△ABC；
（2）由平移性质知，A1A平行于x轴，且等于平移距离4，△A1OA边A1OA上的高可点A1的坐标确定．
试题解析：（1）A（－3，1）， B（0，2），C（－1，4），如图：
（2）A1A=4，OD=1，∴
=
A1A×CD=×4×1=2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A（a，m）在双曲线y=
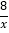上且m＜0，过点A作x轴的垂线，垂足为B．（1）如图1，当a=﹣2时，P（t，0）是x轴上的动点，将点B绕点P顺时针旋转90°至点C，
①若t=1，直接写出点C的坐标；
②若双曲线y=
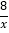经过点C，求t的值．（2）如图2，将图1中的双曲线y=
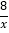（x＞0）沿y轴折叠得到双曲线y=﹣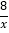（x＜0），将线段OA绕点O旋转，点A刚好落在双曲线y=﹣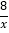（x＜0）上的点D（d，n）处，求m和n的数量关系．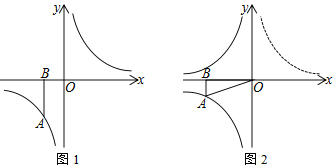
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）解方程：4（x+1）2-169=0；
（2）一圆柱高8cm，底面半径2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程（π取3）是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠ABC=90°．
（1）如图1，分别过A、C两点作经过点B的直线的垂线，垂足分别为M、N，求证：△ABM∽△BCN；
（2）如图2，P是边BC上一点，∠BAP=∠C，tan∠PAC=
，求tanC的值；（3）如图3，D是边CA延长线上一点，AE=AB，∠DEB=90°，sin∠BAC=
，
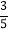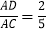，直接写出tan∠CEB的值．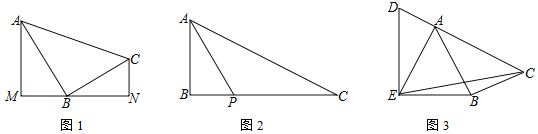
-
科目： 来源： 题型：
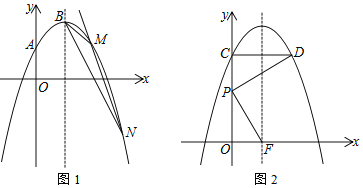
查看答案和解析>>【题目】抛物线L：y=﹣x2+bx+c经过点A（0，1），与它的对称轴直线x=1交于点B．
（1）直接写出抛物线L的解析式；
（2）如图1，过定点的直线y=kx﹣k+4（k＜0）与抛物线L交于点M、N．若△BMN的面积等于1，求k的值；
（3）如图2，将抛物线L向上平移m（m＞0）个单位长度得到抛物线L1，抛物线L1与y轴交于点C，过点C作y轴的垂线交抛物线L1于另一点D．F为抛物线L1的对称轴与x轴的交点，P为线段OC上一点．若△PCD与△POF相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC与△CDE都是等边三角形，B，C，D在一条直线上，连结B，E两点交AC于点M，连结A，D两点交CE于N点．
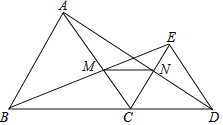
（1）AD与BE有什么数量关系，并证明你的结论．
（2）求证：△MNC是等边三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，BD∥GE，AQ 平分∠FAC，交 BD 于 Q，∠GFA=50°，∠Q=25°，则∠ACB 的 度数（ ）
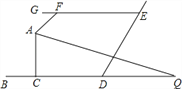
A. 90° B. 95° C. 100° D. 105°
相关试题
