【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
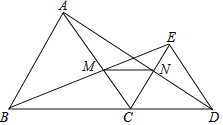
(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
参考答案:
【答案】(1)BE=AD,见解析;(2)见解析.
【解析】
(1)依据等边三角形的性质可得到BE=AD,CE=CD,∠ACB=∠ECD=60°,然后可证明∠ACD=∠BCE=120°,依据SAS可证明△BCE≌△ACD,最后依据全等三角形的性质可得到BE=AD;
(2)证明△BCM≌△ACN,从而得到MC=CN,然后证明∠MCN=60°即可.
(1)BE=AD.理由如下:
∵∠BCA=∠DCE=60°,∴∠BCE=∠ACD.
在△BCE和△ACD中,∵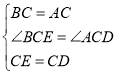 ,∴△BCE≌△ACD(SAS),∴BE=AD;
,∴△BCE≌△ACD(SAS),∴BE=AD;
(2)∵△BCE≌△ACD,∴∠CBM=∠CAN.
∵∠ACB=∠DCE=60°,∴∠ACN=60°,∴∠BCM=∠ACN.
在△BCM和△ACN中,∵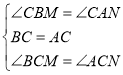 ,∴△BCM≌△ACN(ASA),∴CM=CN.
,∴△BCM≌△ACN(ASA),∴CM=CN.
∵∠ACN=60°,∴△CMN是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=
 ,求tanC的值;
,求tanC的值;(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=
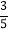 ,
,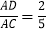 ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.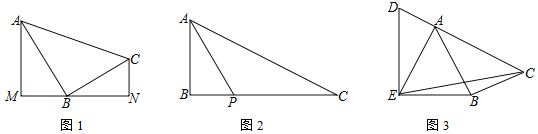
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
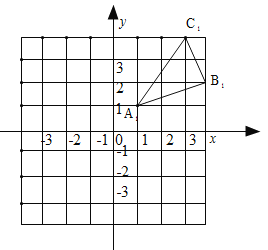
(1)请画出△ABC,并写出点A、B、C的坐标;
(2)求出△AOA1的面积.
-
科目: 来源: 题型:
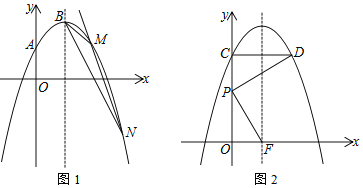
查看答案和解析>>【题目】抛物线L:y=﹣x2+bx+c经过点A(0,1),与它的对称轴直线x=1交于点B.
(1)直接写出抛物线L的解析式;
(2)如图1,过定点的直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.若△BMN的面积等于1,求k的值;
(3)如图2,将抛物线L向上平移m(m>0)个单位长度得到抛物线L1,抛物线L1与y轴交于点C,过点C作y轴的垂线交抛物线L1于另一点D.F为抛物线L1的对称轴与x轴的交点,P为线段OC上一点.若△PCD与△POF相似,并且符合条件的点P恰有2个,求m的值及相应点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD∥GE,AQ 平分∠FAC,交 BD 于 Q,∠GFA=50°,∠Q=25°,则∠ACB 的 度数( )
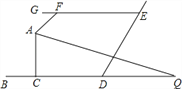
A. 90° B. 95° C. 100° D. 105°
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足条件( )
A. ∠A+∠C=180°B. ∠B+∠D=180°
C. ∠A+∠B=180°D. ∠A+∠D=180°
-
科目: 来源: 题型:
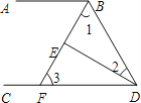
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠3的度数.
相关试题

