【题目】“8字”的性质及应用:
(1)如图①,AD、BC相交于点O,得到一个“8字”ABCD,求证:∠A+∠B=∠C+∠D.
(2)图②中共有多少个“8字”?
(3)如图②,∠ABC和∠ADC的平分线相交于点E,利用(1)中的结论证明∠E=![]() (∠A+∠C).
(∠A+∠C).

参考答案:
【答案】(1)证明见解析;(2)3;(3)证明见解析.
【解析】
(1)根据三角形内角和定理和对顶角相等解答即可;
(2)根据题中给出的“8字”的概念解答即可;
(3)根据角平分线的定义和三角形的外角的性质解答即可.
(1)证明:∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
又∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)解:图②中有:ABCD、BECD、ABED,3个“8字”;
(3)证明:∵BE平分∠ABC,DE平分∠ADC,
∴∠ABE=∠CBE=![]() ∠ABC,∠CDE=∠ADE=
∠ABC,∠CDE=∠ADE=![]() ∠ADC,
∠ADC,
∵∠A+∠ABE=∠E+∠ADE,∠C+∠CDE=∠E+∠CBE,
∴∠E=![]() (∠A+∠C).
(∠A+∠C).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形和1个正方形,第②个图案有7个三角形和2个正方形,第③个图案有10个三角形和3个正方形,…依此规律,第n个图案有 ____________个三角形(用含n的代数式表示);

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个边长为1的正方形纸片分割成7个部分,第①部分是边长不1的正方形纸片面积的一半,第②部分是第①部分面积的半,第③部分是第③部分面积的一半,…,依次类推.
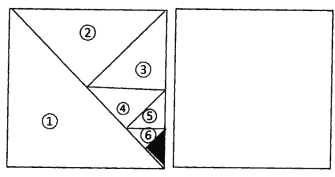
(1)阴影部分的面积是多少?
(2)受此启发,你能求出
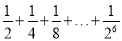 的值吗?
的值吗?(3)请你利用图中右侧的正方形,再设计能求
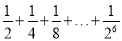 的值的几何图形.(只画出图形即可)
的值的几何图形.(只画出图形即可)(4)根据以上规律,
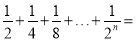 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC。
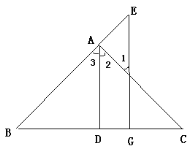
理由如下:
 AD⊥BC于D,EG⊥BC于G,(已知)
AD⊥BC于D,EG⊥BC于G,(已知) ∠ADC=∠EGC=90°,( )
∠ADC=∠EGC=90°,( ) AD‖EG,( )
AD‖EG,( ) ∠1=∠2,( )
∠1=∠2,( )=∠3,(两直线平行,同位角相等)
又
 ∠E=∠1(已知)
∠E=∠1(已知) = (等量代换)
= (等量代换)  AD平分∠BAC( )
AD平分∠BAC( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,m)在双曲线y=
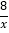 上且m<0,过点A作x轴的垂线,垂足为B.
上且m<0,过点A作x轴的垂线,垂足为B.(1)如图1,当a=﹣2时,P(t,0)是x轴上的动点,将点B绕点P顺时针旋转90°至点C,
①若t=1,直接写出点C的坐标;
②若双曲线y=
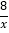 经过点C,求t的值.
经过点C,求t的值.(2)如图2,将图1中的双曲线y=
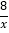 (x>0)沿y轴折叠得到双曲线y=﹣
(x>0)沿y轴折叠得到双曲线y=﹣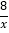 (x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣
(x<0),将线段OA绕点O旋转,点A刚好落在双曲线y=﹣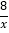 (x<0)上的点D(d,n)处,求m和n的数量关系.
(x<0)上的点D(d,n)处,求m和n的数量关系.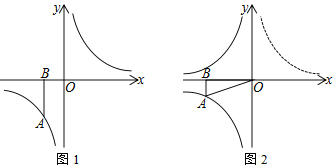
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:4(x+1)2-169=0;
(2)一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=
 ,求tanC的值;
,求tanC的值;(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=
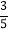 ,
,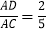 ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.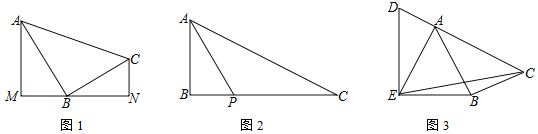
相关试题

