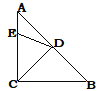
【题目】在等腰Rt△ABC中,D为斜边AB的中点,点E在AC上,且∠EDC=72°,点F在AB上,满足DE=DF,则∠CEF的度数为_______.
参考答案:
【答案】54°或144°
【解析】分析:分两种情况:①点F在AD上时,可求出∠DEF=81°,在△CDE中可求出∠CED=63°,故可求出∠CEF=144°;②点F在DB上时,可求出∠DEF=9°,故可求出∠CEF=54°.
详解:①点F在AD上时,如图1,
∵AC=BC,D是AB的中点,且∠ACB=90°,
∴∠ADC=90°,∠DCE=45°
∵∠CDE=72°
∴∠EDF=18°
∵DE=DF
∴∠DEF=81°
在△ECD中,∠CDE=72°,∠ECD=45°
∴∠CED=63°,
∴∠CEF=144°;
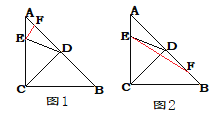
②点F在DB上时,如图2.
同理得,∠DEF=9°,
∴∠CEF=54°.
故答案为:54°或144°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车相遇后都停下来休息,快车休息2个小时后,以原速的
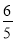 继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的
继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的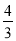 返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.
返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.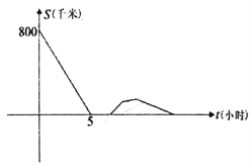
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,点G为边BC的中点,点D从点C出发沿CA向点A运动,到点A停止,以GD为边作正方形DEFG,则点E运动的路程为_______.
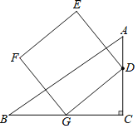
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
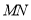 与直线
与直线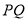 垂直相交于点
垂直相交于点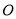 ,点
,点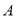 在射线
在射线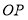 上运动(点
上运动(点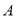 不与点
不与点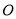 重合),点
重合),点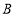 在射线
在射线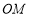 上运动(点
上运动(点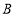 不与点
不与点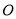 重合).
重合).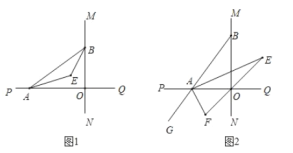
(1)如图1,已知
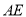 、
、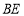 分别是
分别是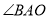 和
和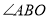 的角平分线,
的角平分线,①当
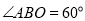 时,求
时,求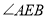 的度数;
的度数;②点
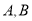 在运动的过程中,
在运动的过程中,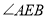 的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出
的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出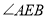 的大小;
的大小;(2)如图2,延长
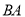 至
至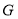 ,已知
,已知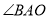 、
、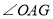 的角平分线与
的角平分线与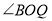 的角平分线所在的直线分别相交于
的角平分线所在的直线分别相交于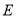 、
、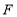 ,在
,在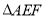 中,如果有一个角是另一个角的3倍,请直接写出
中,如果有一个角是另一个角的3倍,请直接写出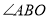 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)某中学组织学生去福利院慰问,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)求甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2000元,那么最多可购买多少个甲礼品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=k1x+b与反比例函数y=
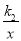 的图象交于第一象限内P(
的图象交于第一象限内P(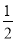 ,8),Q(4,m)两点.
,8),Q(4,m)两点.(1)分别求出这两个函数的表达式;
(2)请直接写出不等式k1x+b<
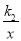 的解集.
的解集.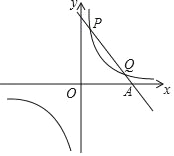
相关试题

