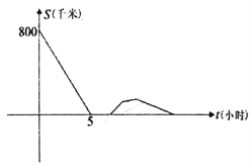
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车相遇后都停下来休息,快车休息2个小时后,以原速的![]() 继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的
继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的![]() 返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.
返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.
参考答案:
【答案】620
【解析】
设慢车的速度为a千米/时,快车的速度为b千米/时,根据题意可得5(a+b)=800,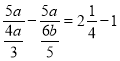 ,联立求出a、b的值即可解答.
,联立求出a、b的值即可解答.
解:设慢车的速度为a千米/时,快车的速度为b千米/时,由图可知两车5个小时后相遇,且总路程为800千米,则5a+5b=800,即a+b=160,
再根据题意快车休息2个小时后,以原速的![]() 继续向甲行驶,则快车到达甲地的时间为:
继续向甲行驶,则快车到达甲地的时间为:
![]() ,同理慢车回到甲地的时间为:
,同理慢车回到甲地的时间为:![]() ,而快车比慢车早到2.25小时,但是由题意知快车为休息2小时出发而慢车是休息3小时,即实际慢车比快车晚出发1小时,即实际快车到甲地所花时间比慢车快2.25-1=1.25小时,
,而快车比慢车早到2.25小时,但是由题意知快车为休息2小时出发而慢车是休息3小时,即实际慢车比快车晚出发1小时,即实际快车到甲地所花时间比慢车快2.25-1=1.25小时,
即: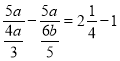 ,化简得5a=3b,
,化简得5a=3b,
联立得![]() ,解得
,解得![]() ,
,
所以两车相遇的时候距离乙地为![]() =500千米,
=500千米,
快车到位甲地的时间为![]() =2.5小时,
=2.5小时,
而慢车比快车多休息一个小时则此时慢车应该往甲地行驶了1.5小时,此时慢车往甲地行驶了![]() =120千米,所以此时慢车距离乙地为500+120=620千米,
=120千米,所以此时慢车距离乙地为500+120=620千米,
即快车到达甲地时,慢车距乙地620千米.
故答案为:620.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=mx+n与反比例函数y=
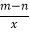 ,其中mn<0,m、n均为常数,它们在同一坐标系中的图象可以是( )
,其中mn<0,m、n均为常数,它们在同一坐标系中的图象可以是( )A.
 B.
B. 
C.
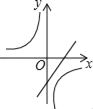 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在三角形
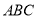 中,
中, ,
, ,
,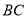 边绕点
边绕点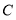 按逆时针方向旋转一周回到原来的位置(即旋转角
按逆时针方向旋转一周回到原来的位置(即旋转角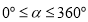 ),在旋转过程中(图2),当
),在旋转过程中(图2),当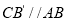 时,旋转角为________度;当
时,旋转角为________度;当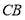 所在直线垂直于
所在直线垂直于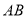 时,旋转角为__________度.
时,旋转角为__________度.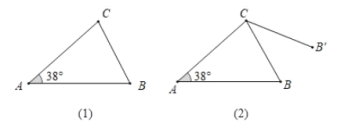
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,点G为边BC的中点,点D从点C出发沿CA向点A运动,到点A停止,以GD为边作正方形DEFG,则点E运动的路程为_______.
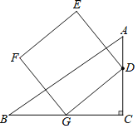
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
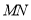 与直线
与直线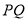 垂直相交于点
垂直相交于点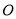 ,点
,点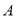 在射线
在射线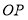 上运动(点
上运动(点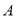 不与点
不与点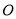 重合),点
重合),点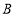 在射线
在射线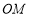 上运动(点
上运动(点 不与点
不与点 重合).
重合).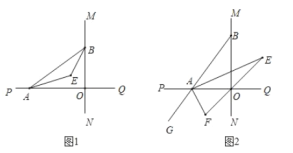
(1)如图1,已知
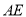 、
、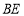 分别是
分别是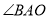 和
和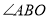 的角平分线,
的角平分线,①当
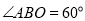 时,求
时,求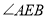 的度数;
的度数;②点
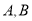 在运动的过程中,
在运动的过程中,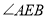 的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出
的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出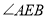 的大小;
的大小;(2)如图2,延长
 至
至 ,已知
,已知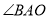 、
、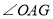 的角平分线与
的角平分线与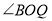 的角平分线所在的直线分别相交于
的角平分线所在的直线分别相交于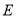 、
、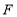 ,在
,在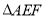 中,如果有一个角是另一个角的3倍,请直接写出
中,如果有一个角是另一个角的3倍,请直接写出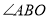 的度数.
的度数. -
科目: 来源: 题型:
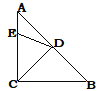
查看答案和解析>>【题目】在等腰Rt△ABC中,D为斜边AB的中点,点E在AC上,且∠EDC=72°,点F在AB上,满足DE=DF,则∠CEF的度数为_______.
相关试题

