【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路:
(1)请你按照他们的解题思路过程完成解答过程;
(2)填空:在△DEF中,DE=15,EF=13,DF=4,则△DEF的面积是 .
参考答案:
【答案】
(1)解:如图,在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则CD=14﹣x,
由勾股定理得:AD2=AB2﹣BD2=152﹣x2,AD2=AC2﹣CD2=132﹣(14﹣x)2,
故152﹣x2=132﹣(14﹣x)2,
解得:x=9.
∴AD=12.
∴S△ABC= ![]() BCAD=
BCAD= ![]() ×14×12=84
×14×12=84

(2)24
【解析】(2)如图,在△DEF中,DE=15,EF=13,DF=4, 设GD=x,则GE=15﹣x,
由勾股定理得:FG2=DF2﹣GD2=42﹣x2 , FG2=EF2﹣EG2=132﹣(15﹣x)2 ,
故42﹣x2=132﹣(15﹣x)2 ,
解得:x=2.4.
∴FG=3.2.
∴S△DEF= ![]() DEFG=
DEFG= ![]() ×15×3.2=24.
×15×3.2=24.
所以答案是:24.
(1)根据题意利用勾股定理表示出AD2的值,进而得出等式求出答案;(2)根据题意利用勾股定理表示出FG2的值,进而得出等式求出答案.
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题 大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此  的小数部分我们不可能全部地写出来,但是由于
的小数部分我们不可能全部地写出来,但是由于
1< <2,所以
<2,所以  的整数部分为1,将
的整数部分为1,将  减去其整数部分1,所得的差就是其小数部分
减去其整数部分1,所得的差就是其小数部分  ﹣1,根据以上的内容,解答下面的问题:
﹣1,根据以上的内容,解答下面的问题:
(1)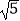 的整数部分是 , 小数部分是;
的整数部分是 , 小数部分是;
(2)1+ 的整数部分是 , 小数部分是;
的整数部分是 , 小数部分是;
(3)1+ +
+ 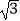 整数部分是 , 小数部分是;
整数部分是 , 小数部分是;
(4)若设2+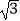 整数部分是x,小数部分是y,求x﹣
整数部分是x,小数部分是y,求x﹣ 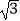 y的值.
y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地市话的收费标准为: ①通话时间在3分钟以内(包括3分钟)话费0.3元;
②通话时间超过3分钟时,超过部分的话费按每分钟0.11元计算.
在一次通话中,如果通话时间超过3分钟,那么话费y(元)与通话时间x(分)之间的关系式为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD交于点O,CE∥BD,DE∥AC.
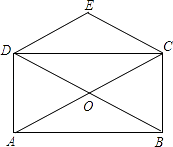
(1)证明:四边形OCED为菱形;
(2)若AC=4,求四边形CODE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一元二次方程x2+px﹣2=0的一个根为2,则p=_____,另一个根是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 4a3·2a2=8a6 B. (-2x4)·(-3x4)=6x8
C. 5x3·3x4=8x7 D. (-x)·(-2x)2·(-3x)3=-108x6
-
科目: 来源: 题型:
查看答案和解析>>【题目】动手操作:请按要求作图.(规范作图,保留作图痕迹即可,不要求尺规作图)
(
 )如图(
)如图( ),
), 是
是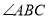 内一定点,
内一定点, 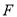 为射线
为射线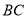 边上一定点,请在射线
边上一定点,请在射线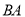 上找一点
上找一点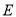 ,使得
,使得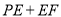 最小.
最小.(
 )如图(
)如图(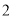 ),
),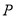 是
是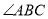 内一定点,点
内一定点,点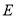 、
、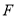 分别为射线
分别为射线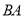 、
、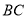 边上两个动点,请作出使得
边上两个动点,请作出使得 最小的
最小的 点和
点和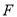 点.
点.(
 )如图(
)如图(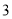 ),
),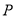 是
是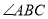 内一定点,点
内一定点,点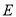 、
、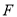 分别为射线
分别为射线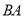 、
、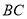 边上两个动点,请作出使得
边上两个动点,请作出使得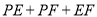 最小的
最小的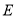 点和
点和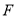 点.
点.拓展应用:
(
 )如图(
)如图(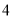 ),
),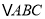 为锐角三角形,
为锐角三角形, 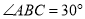 ,
,  ,
, 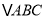 的面积为
的面积为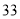 ,点
,点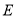 、
、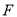 、
、 分别为
分别为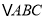 三边
三边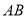 、
、 、
、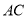 上的三个动点,请在图中作出满足条件的周长最小的
上的三个动点,请在图中作出满足条件的周长最小的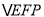 ,并求出
,并求出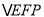 周长的最小值.
周长的最小值.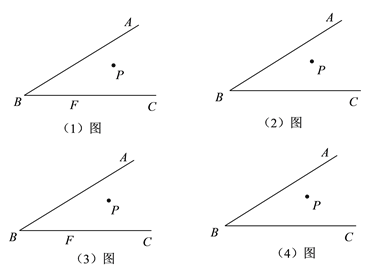
相关试题

