【题目】如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
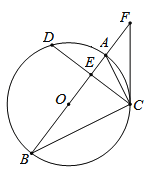
(1)求证:CF是⊙O的切线.
(2)若AC=4,tan∠ACD![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)利用圆周角定理以及等腰三角形的性质得出∠OCF=90°,进而得出答案;
(2)利用垂径定理推论得出![]() ,进而得出BC的长,再利用勾股定理求出即可.
,进而得出BC的长,再利用勾股定理求出即可.
试题解析:(1)连接CO,
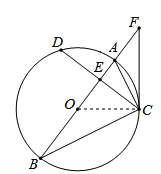
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠ACO+∠OCB=90°,
∵OB=CO,
∴∠B=∠OCB,
∵∠FCA=∠B,
∴∠BCO=∠ACF,
∴∠OCA+∠ACF=90°,
即∠OCF=90°,
∴CF是⊙O的切线;
(2)∵直径AB平分弦CD,
∴AB⊥DC,
∴![]() ,
,
∵AC=4,tan∠ACD=![]() ,
,
∴tan∠B=tan∠ACD=![]() ,
,
∴![]()
∴BC=8,
∴在Rt△ABC中,
AB=![]()
则⊙O的半径为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为6cm的⊙O中,点A是劣弧
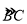 的中点,点D是优弧
的中点,点D是优弧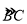 上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论: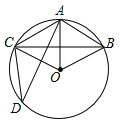
①OA⊥BC;②BC=
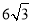 cm;③sin∠AOB=
cm;③sin∠AOB=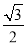 ;④四边形ABOC是菱形.其中正确结论的序号是( )
;④四边形ABOC是菱形.其中正确结论的序号是( )A.①③ B.①②③④ C.②③④ D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 和直线
和直线 .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.下列判断: ①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x= 1 .其中正确的有( )
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.下列判断: ①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x= 1 .其中正确的有( ) 
A.1个 B.2个 C. 3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=x+1的图象与反比例函数y2=
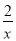 的图象交于A、B两点,过点作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO、BO,下列说法正确的是( )
的图象交于A、B两点,过点作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO、BO,下列说法正确的是( )
A.点A和点B关于原点对称 B.当x<1时,y1>y2
C.S△AOC=S△BOD D.当x>0时,y1、y2都随x的增大而增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:


小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
(2)小聪的作法正确吗?请说明理由.
(3)请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中正确的是 ( )
A. |-3|=-|3| B. |-1)=-(-1) C. |-2|<|-1| D. -|+2|=+|-2|
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列对二次函数y=2(x+4)2的增减性描述正确的是( )
A. 当x>0时,y随x的增大而减小
B. 当x<0时,y随x的增大而增大
C. 当x>-4时,y随x的增大而减少
D. 当x<-4时,y随x的增大而减少
相关试题

