搜索
【题目】下列图形中，既是中心对称图又是轴对称图形的是（ ）
A.
B.
C.
D.
参考答案：
【答案】C
【解析】解：A、是轴对称图形，不是中心对称图形，故本选项错误；
B、是中心对称图，不是轴对称图形，故本选项错误；
C、既是中心对称图又是轴对称图形，故本选项正确；
D、是轴对称图形，不是中心对称图形，故本选项错误．
故选C．
【考点精析】掌握轴对称图形和中心对称及中心对称图形是解答本题的根本，需要知道两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴；如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，湿地景区岸边有三个观景台A、B、C，已知AB=1400米，AC=1000米，B点位于A点的南偏西60.7°方向，C点位于A点的南偏东66.1°方向．
（1）求△ABC的面积；
（2）景区规划在线段BC的中点D处修建一个湖心亭，并修建观景栈道AD，试求A、D间的距离．（结果精确到0.1米）
（参考数据：sin53.2°≈0.80，cos53.2°≈0.60，sin60.7°≈0.87，cos60.7°≈0.49，sin66.1°≈0.91，cos66.1°≈0.41，
≈1.414）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知二次函数y=ax2+bx+3（a≠0）的图象经过点A（3，0），B（4，1），且与y轴交于点C，连接AB、AC、BC．
（1）求此二次函数的关系式；
（2）判断△ABC的形状；若△ABC的外接圆记为⊙M，请直接写出圆心M的坐标；
（3）若将抛物线沿射线BA方向平移，平移后点A、B、C的对应点分别记为点A1、B1、C1 ， △A1B1C1的外接圆记为⊙M1 ， 是否存在某个位置，使⊙M1经过原点？若存在，求出此时抛物线的关系式；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】问题呈现：
（Ⅰ）如图1，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上，AE=DG，求证：2S四边形EFGH=S矩形ABCD ． （S表示面积）
（Ⅱ）实验探究：某数学实验小组发现：若图1中AH≠BF，点G在CD上移动时，上述结论会发生变化，分别过点E、G作BC边的平行线，再分别过点F、H作AB边的平行线，四条平行线分别相交于点A1、B1、C1、D1 ， 得到矩形A1B1C1D1 ．
如图2，当AH＞BF时，若将点G向点C靠近（DG＞AE），经过探索，发现：2S四边形EFGH=S矩形ABCD+S
．
如图3，当AH＞BF时，若将点G向点D靠近（DG＜AE），请探索S四边形EFGH、S矩形ABCD与S 之间的数量关系，并说明理由．
（Ⅲ）迁移应用：
请直接应用“实验探究”中发现的结论解答下列问题：
⑴如图4，点E、F、G、H分别是面积为25的正方形ABCD各边上的点，已知AH＞BF，AE＞DG，S四边形EFGH=11，HF=
，求EG的长．
⑵如图5，在矩形ABCD中，AB=3，AD=5，点E、H分别在边AB、AD上，BE=1，DH=2，点F、G分别是边BC、CD上的动点，且FG=
，连接EF、HG，请直接写出四边形EFGH面积的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，∠A=30°，BC=4，以点C为圆心，CB长为半径作弧，交AB于点D；再分别以点B和点D为圆心，大于
BD的长为半径作弧，两弧相交于点E，作射线CE交AB于点F，则AF的长为（ ） 
A.5
B.6
C.7
D.8 -
科目： 来源： 题型：
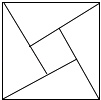
查看答案和解析>>【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）2=21，大正方形的面积为13，则小正方形的面积为（ ）
A.3
B.4
C.5
D.6 -
科目： 来源： 题型：
查看答案和解析>>【题目】在半径为1的⊙O中，弦AB、AC的长分别为1和
，则∠BAC的度数为 ．
相关试题
