【题目】已知:△ABC中,AB=AC,∠B=α.
(1)如图1,点D,E分别在边AB,AC上,线段DE的垂直平分线MN交直线BC于点M,交DE于点N,求证:BD+CE=BC.需补充条件∠EMN=(用含α的式子表示)补充条件后并证明;
(2)把(1)中的条件改为点D,E分别在边BA、AC延长线上,线段DE的垂直平分线MN交直线BC于点M,交DE于点N(如图2),并补充条件∠EMN=(用含α的式子表示),通过观察或测量,猜想线段BD,CE与BC之间满足的数量关系,并予以证明.
参考答案:
【答案】
(1)![]()
α
(2)![]()
α
【解析】解:(1)当∠EMN= ![]() α时,BD+CE=BC.
α时,BD+CE=BC.
理由:如图1所示:连接DM.
∵AB=AC,
∴∠B=∠C=α.
∵MN是DE的垂直平分线,
∴DN=NE,DM=EM.
在△MND和△MNE中, ,
,
∴△MND≌△MNE.
∴∠DMN=∠EMN= ![]() α.
α.
∴∠DME=α.
∵∠C+∠CEM=∠DMB+∠DME,∠C=∠DME=α,
∴∠DMB=∠CEM.
在△BDM和△CME中, ,
,
∴△BDM≌△CME.
∴BD=MC,EC=BM.
又∵MB+MC=BC,
∴BD+EC=BC.
2)当∠EMN= ![]() α时,BD=CE+BC.
α时,BD=CE+BC.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠DBM=∠MCE.
∵MN是DE的垂直平分线,
∴DN=NE,DM=EM.
在△MND和△MNE中, ,
,
∴△MND≌△MNE.
∴∠DMN=∠EMN= ![]() α.
α.
∴∠EMD=∠B=α
∵∠BMD+∠MDB=α,∠EMC+∠CMD=α,
∴∠EMC=∠MDB.
在△BDM和△CME中, ,
,
∴△BDM≌△CME.
∴BD=MC,EC=BM.
又∵MB+BC=MC,
∴EC+BC=BD.
(1)当∠EMN= ![]() α时,BD+CE=BC.连接DM.先证明∠DME=α.接下来证明∠DMB=∠CEM.然后依据AAS可证明△BDM≌△CME,然后由全等三角形的性质可证得BD=MC,EC=BM,结合条件MB+MC=BC,可证得问题的结论;(2)当∠EMN=
α时,BD+CE=BC.连接DM.先证明∠DME=α.接下来证明∠DMB=∠CEM.然后依据AAS可证明△BDM≌△CME,然后由全等三角形的性质可证得BD=MC,EC=BM,结合条件MB+MC=BC,可证得问题的结论;(2)当∠EMN= ![]() α时,BD=CE+BC.先证明∠DMN=∠EMN=
α时,BD=CE+BC.先证明∠DMN=∠EMN= ![]() α.从而得到∠EMD=∠B=α,接下来,依据等角的补角相等可证得∠DBM=∠MCE,然后依据三角形的外角的性质和角的和差关系证明∠MDB=∠EMC,然后依据AAS可证明△BDM≌△CME,由全等三角形的性质可得到BD=MC,EC=BM,结合MB+BC=MC可证得EC+BC=BD.
α.从而得到∠EMD=∠B=α,接下来,依据等角的补角相等可证得∠DBM=∠MCE,然后依据三角形的外角的性质和角的和差关系证明∠MDB=∠EMC,然后依据AAS可证明△BDM≌△CME,由全等三角形的性质可得到BD=MC,EC=BM,结合MB+BC=MC可证得EC+BC=BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F.
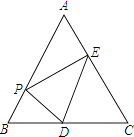
(1)求∠APE的度数;
(2)连接DE,当△PDE为等边三角形时,求BP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于一元二次方程2x2+1=3x,下列说法错误的是( )
A.二次项系数是2
B.一次项系数是3
C.常数项是1
D.x=1是它的一个根 -
科目: 来源: 题型:
查看答案和解析>>【题目】用频数分布直方图描述数据,下列说法正确的是( )
A. 所分的组数与数据的个数无关
B. 长方形的高越高,说明落在这个区域的数据越多
C. 可以不求最大值和最小值的差
D. 可以看出数据的变化趋势
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(﹣3x2y)3=﹣9x6y3
B.(a+b)(a+b)=a2+b2
C.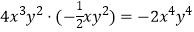
D.(x2)3=x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是( )
A. a<2且a≠0B. a>2C. a<2且a≠1D. a<﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】把不等式组
 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.
B.
C.
D.
相关试题

