【题目】对于一元二次方程![]() ,有下列说法:
,有下列说法:
①若![]() ,则方程
,则方程![]() 必有一个根为1;
必有一个根为1;
②若方程![]() 有两个不相等的实根,则方程
有两个不相等的实根,则方程![]() 必有两个不相等的实根;
必有两个不相等的实根;
③若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;
成立;
④若![]() 是一元二次方程
是一元二次方程![]() 的根,则
的根,则![]() .
.
其中正确的有( )
A.1个B.2个C.3个D.4个
参考答案:
【答案】A
【解析】
按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论,可得答案.
解:①若x=1时,方程ax2+bx+c=0,则a+b+c=0,
∵无法确定a-b+c=0.故①错误;
②∵方程ax2+c=0有两个不相等的实根,
∴△=0-4ac>0
∴-4ac>0
则方程ax2+bx+c=0的判别式,
△=b2-4ac>0
∴方程ax2+bx+c=0必有两个不相等的实根,故②正确;
③∵c是方程ax2+bx+c=0的一个根,
则ac2+bc+c=0
∴c(ac+b+1)=0
若c=0,等式仍然成立,
但ac+b+1=0不一定成立,故③错误;
④若x0是一元二次方程ax2+bx+c=0的根,
则由求根公式可得:
![]() 或
或![]() ,
,
∴![]() 或
或![]()
∴b24ac=(2ax0+b)2,故④错误.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
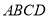 中,对角线
中,对角线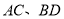 相交于点
相交于点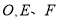 是对角线
是对角线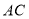 上的两点,给出下列四个条件:①
上的两点,给出下列四个条件:①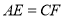 ;②
;②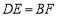 ;③
;③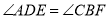 ;④
;④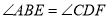 .其中能判定四边形
.其中能判定四边形 是平行四边形的有( )
是平行四边形的有( )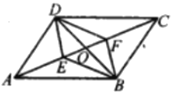
A.①B.①④C.①③④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业前年按可回收垃圾处理费15元/吨、不可回收垃圾处理费25元/吨的收费标准,共支付两种垃圾处理费5000元,从去年元月起,收费标准上调为:可回收垃圾处理费30元/吨,不可回收垃圾处理费100元/吨.若该企业去年处理的这两种垃圾数量与前年相比没有变化,但调价后就要多支付处理费9000元.
(1)该企业前年处理的可回收垃圾和不可回收垃圾各多少吨?
(2)该企业计划今年将上述两种垃圾处理总量减少到200吨,且可回收垃圾不少于不可回收垃圾处理量的3倍,则今年该企业至少有多少吨可回收垃圾?
-
科目: 来源: 题型:
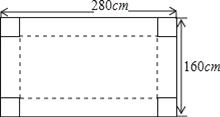
查看答案和解析>>【题目】我国水资源比较缺乏,人均水量约为世界人均水量的四分之一,其中西北地区缺水尤为严重.一村民为了蓄水,他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水.已知白铁皮的长为280cm,宽为160cm(如图).
(1)若水箱的底面积为16000cm2,请求出切去的小正方形边长;
(2)对(1)中的水箱,若盛满水,这时水量是多少升?(注:1升水=1000cm3水)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 、
、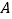 在数轴上表示的数分别是
在数轴上表示的数分别是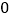 ,
,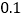 ,将线段
,将线段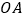 分成
分成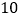 等分,离
等分,离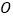 点最近的分点为
点最近的分点为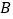 ;再将线段
;再将线段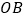 分成
分成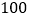 等份,其分点由左向右依次为
等份,其分点由左向右依次为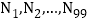 ;继续将线段
;继续将线段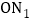 分成
分成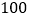 等份,其分点由左向右依次为
等份,其分点由左向右依次为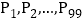 ;
;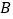 对应的数用科学记数法表示为:________;
对应的数用科学记数法表示为:________;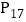 对应的数用科学记数法表示为:______.
对应的数用科学记数法表示为:______.
-
科目: 来源: 题型:
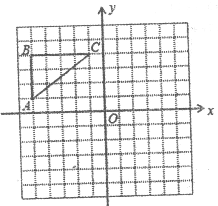
查看答案和解析>>【题目】如图,在正方形网络中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
画出△ABC关于
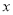 轴对称的△A1B1C1;
轴对称的△A1B1C1;画出△ABC关于原点O对称的△A2B2C2;
点C1的坐标是 ;点C2的坐标是 ;
试判断:△A1B1C1与△A2B2C2是否关于y轴对称?(只需写出判断结果)
-
科目: 来源: 题型:
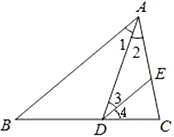
查看答案和解析>>【题目】完成下面的推理填空
如图,已知
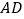 是
是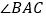 的角平分线,
的角平分线,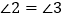 ,试证明:
,试证明: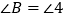 .
.
证明:
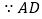 是
是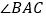 的角平分线(已知)
的角平分线(已知) ___________( )
___________( )又
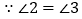 (已知)
(已知) ___________( )
___________( ) ___________( )
___________( ) ___________( )
___________( )
相关试题

