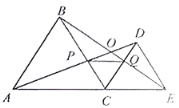
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 重合),在
重合),在![]() 同侧分别作等边三角形
同侧分别作等边三角形![]() 和等边三角形
和等边三角形![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是等边三角形,恒成立的是______.
是等边三角形,恒成立的是______.
参考答案:
【答案】①②③④
【解析】
①由△ABC和△CDE都是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,所以∠ACD=∠BCE=120°,所以△ACD≌△BCE(SAS),从而AD=BE,故①正确;②④由△ACD≌△BCE得∠CBE=∠DAC,加之AC=BC,易得∠ACB=∠BCQ=60°,可证△CQB≌△CPA(ASA),从而CP=CQ,再加之∠PCQ=60°,可推出△PCQ为等边三角形,易得∠PQC=60°=∠DCE,根据内错角相等,两直线平行,可知②④正确;③结合△ACD≌△BCE和三角形的外角的性质,可得∠AOB=60°,故③正确.
解:①∵等边△ABC和等边△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
∵在△ACD与△BCE中,

∴△ACD≌△BCE(SAS),
∴AD=BE,
故①正确;
④②∵△ACD≌△BCE,
∴∠CBE=∠DAC,
∵由∠ACB=∠DCE=60°得∠BCD=60°,
∴∠ACP=∠BCQ,
又∵AC=BC,
∴△CQB≌△CPA(ASA),
∴CP=CQ,
又∵∠PCQ=60°
∴△PCQ为等边三角形,
∴∠PQC=60°,
∴∠PQC=60°=∠DCE
∴PQ∥AE
故②④正确;

③∵△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB,
又∵∠ACB=∠CBE+∠CEB=60°,
∴∠AOB=∠ACB=60°,
故③正确.
故答案为:①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个外角为100°,则这个等腰三角形的顶角为________;等腰三角形一腰上的高与腰的夹角为36°,则该等腰三角形的顶角为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
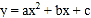 的图象开口向上,图象经过点
的图象开口向上,图象经过点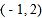 和
和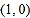 ,且与
,且与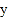 轴相交于负半轴.
轴相交于负半轴.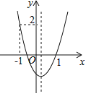
第
 问:给出四个结论:①
问:给出四个结论:①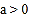 ;②
;②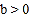 ;③
;③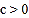 ;④
;④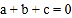 .写出其中正确结论的序号(答对得
.写出其中正确结论的序号(答对得 分,少选、错选均不得分)
分,少选、错选均不得分)第
 问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号. -
科目: 来源: 题型:
查看答案和解析>>【题目】某童装店在服装销售中发现:进货价每件60元,销售价每件100元的某童装每天可售出20件
 为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利
为了迎接“六一儿童节”,童装店决定采取适当的促销措施,扩大销售量,增加盈利 经调查发现:如果每件童装降价1元,那么每天就可多售出2件.
经调查发现:如果每件童装降价1元,那么每天就可多售出2件. 如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元?
如果童装店想每天销售这种童装盈利1050元,同时又要使顾客得到更多的实惠,那么每件童装应降价多少元? 每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元?
每件童装降价多少元时,童装店每天可获得最大利润?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在
 中,
中,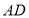 是高,
是高,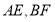 是角平分线,它们相交于点
是角平分线,它们相交于点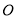 ,
,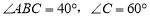 .求
.求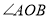 和
和 的度数.
的度数.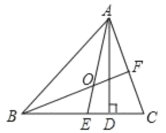
(2)一个多边形的内角和是外角和的3倍,它是几边形?若这个多边形的各个内角都相等,求这个多边形的每个内角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
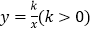 的图象与直线
的图象与直线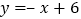 相交于第一象限
相交于第一象限 、
、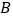 的两点.如图所示,过
的两点.如图所示,过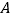 、
、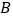 两点分别作
两点分别作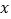 、
、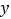 轴的垂线,线段
轴的垂线,线段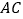 、
、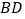 相交与
相交与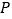 ,给出以下结论:①
,给出以下结论:①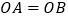 ;②四边形
;②四边形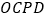 是正方形;③若
是正方形;③若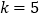 .则
.则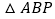 的面积是
的面积是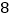 ;④
;④ 点一定在直线
点一定在直线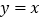 上,其中正确命题的个数是几个( )
上,其中正确命题的个数是几个( )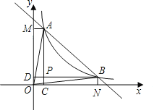
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
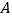 、
、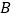 是双曲线
是双曲线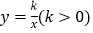 上的点,
上的点,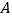 、
、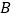 两点的横坐标分别是
两点的横坐标分别是 、
、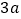 ,线段
,线段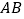 的延长线交
的延长线交 轴于点
轴于点 ,若
,若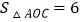 ,则
,则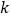 的值为( )
的值为( )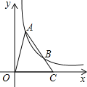
A. 2 B. 3 C. 4 D. 6
相关试题

