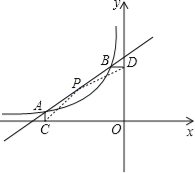
【题目】如图,已知A![]() ,B(-1,2)是一次函数
,B(-1,2)是一次函数![]() 与反比例函数
与反比例函数![]()
(![]() )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.

参考答案:
【答案】(1)当﹣4<x<﹣1时,一次函数大于反比例函数的值;
(2)一次函数的解析式为y=![]() x+
x+![]() ;m=﹣2;
;m=﹣2;
(3)P点坐标是(﹣![]() ,
,![]() ).
).
【解析】
试题(1)根据一次函数图象在反比例函数图象上方的部分是不等式的解,观察图象,可得答案;
(2)根据待定系数法,可得函数解析式以及m的值;
(3)设P的坐标为(x,![]() x+
x+![]() )如图,由A、B的坐标可知AC=
)如图,由A、B的坐标可知AC=![]() ,OC=4,BD=1,OD=2,易知△PCA的高为x+4,△PDB的高(2﹣
,OC=4,BD=1,OD=2,易知△PCA的高为x+4,△PDB的高(2﹣![]() x﹣
x﹣![]() ),由△PCA和△PDB面积相等得,可得答案.
),由△PCA和△PDB面积相等得,可得答案.
试题解析:(1)由图象得一次函数图象在反比例函数图象上方时,﹣4<x<﹣1,
所以当﹣4<x<﹣1时,一次函数大于反比例函数的值;
(2)设一次函数的解析式为y=kx+b,
y=kx+b的图象过点(﹣4,![]() ),(﹣1,2),则
),(﹣1,2),则
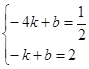 ,
,
解得![]()
一次函数的解析式为y=![]() x+
x+![]() ,
,
反比例函数y=![]() 图象过点(﹣1,2),
图象过点(﹣1,2),
m=﹣1×2=﹣2;
(3)连接PC、PD,如图,设P的坐标为(x,![]() x+
x+![]() )如图,由A、B的坐标可知AC=
)如图,由A、B的坐标可知AC=![]() ,OC=4,BD=1,OD=2,易知△PCA的高为x+4,△PDB的高(2﹣
,OC=4,BD=1,OD=2,易知△PCA的高为x+4,△PDB的高(2﹣![]() x﹣
x﹣![]() ),由△PCA和△PDB面积相等得
),由△PCA和△PDB面积相等得
![]() ×
×![]() ×(x+4)=
×(x+4)=![]() ×|﹣1|×(2﹣
×|﹣1|×(2﹣![]() x﹣
x﹣![]() ),
),
x=﹣![]() ,y=
,y=![]() x+
x+![]() =
=![]() ,
,
∴P点坐标是(﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】安九高铁潜山段有甲、乙两个施工队,现中标承建安九高铁一段建设工程.若让两队合作,
 天可以完工,需要费用
天可以完工,需要费用 万元;若让两队合作
万元;若让两队合作 天后,剩下的工程由甲队做,还需
天后,剩下的工程由甲队做,还需 天才能完成,这样只需要费用
天才能完成,这样只需要费用 万元.
万元.(1)甲、乙两队单独完成此项工程各需多少天?
(2)甲、乙两队单独完成此项工程各需费用多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的角满足下列条件:①
的角满足下列条件:① ;②
;② ,
, ;③
;③ ;④
;④ ,
, ,其中一定不是直角三角形的是______.(只填序号)
,其中一定不是直角三角形的是______.(只填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
 的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=
 的图象上,当-3≤x≤-1时,求函数值y的取值范围.
的图象上,当-3≤x≤-1时,求函数值y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,正比例函数
 的图象与反比例函数
的图象与反比例函数 的图象交于点
的图象交于点

(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当
 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值?(3)
 是反比例函数图象上的一动点,其中
是反比例函数图象上的一动点,其中 过点
过点 作直线
作直线 轴,交
轴,交 轴于点
轴于点 ;过点
;过点 作直线
作直线 轴交
轴交 轴于点
轴于点 ,交直线
,交直线 于点
于点 .当四边形
.当四边形 的面积为6时,请判断线段
的面积为6时,请判断线段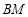 与
与 的大小关系,并说明理由.
的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图象与反比例函数
的图象与反比例函数 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的 ,
, 两点,与
两点,与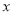 轴交于点
轴交于点 .
.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当
 时,
时,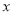 的取值范围;
的取值范围;(3)在
 轴上找一点
轴上找一点 使
使 最大,求
最大,求 的最大值及点
的最大值及点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有长为24m的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10m).

(1)如果所围成的花圃的面积为45m2,试求宽AB的长;
(2)按题目的设计要求,能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
相关试题

