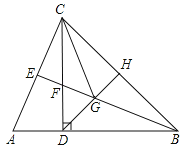
【题目】如图,在△ABC中,AB=BC,CD⊥AB于点D,CD=BD,BE平分∠ABC,点H是BC边的中点,连接DH,交BE于点G,连接CG.
(1)求证:△ADC≌△FDB;
(2)求证:CE=![]() BF;
BF;
(3)判断△ECG的形状,并证明你的结论;
(4)猜想BG与CE的数量关系,并证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)△ECG为等腰直角三角形;(4)GB=![]() CE.
CE.
【解析】
试题分析:(1)首先根据AB=BC,BE平分∠ABC,得到BE⊥AC,CE=AE,进一步得到∠ACD=∠DBF,结合CD=BD,即可证明出△ADC≌△FDB;
(2)由△ADC≌△FDB得到AC=BF,结合CE=AE,即可证明出结论;
(3)由点H是BC边的中点,得到GH垂直平分BC,即GC=GB,由∠DBF=∠GBC=∠GCB=∠ECF,得∠ECO=45°,结合BE⊥AC,即可判断出△ECG的形状;
(4)由△ECG为等腰直角三角形,得到GC=![]() CE,因为GC=GB,即可得到GB=
CE,因为GC=GB,即可得到GB=![]() CE.
CE.
试题解析:(1)∵AB=BC,BE平分∠ABC,∴BE⊥AC,CE=AE,∵CD⊥AB,∴∠ACD=∠DBF,在△ADC和△FDB中,∵∠ACD=∠DFB,CD=BD,∠ADC=∠BDF,∴△ADC≌△FDB(ASA);
(2)∵△ADC≌△FDB,∴AC=BF,又∵CE=AE,∴CE=![]() BF;
BF;
(3)△ECG为等腰直角三角形.∵点H是BC边的中点,∴GH垂直平分BC,∴GC=GB,∵∠DBF=∠GBC=∠GCB=∠ECF,得∠ECG=45°,又∵BE⊥AC,∴△ECG为等腰直角三角形;
(4)GB=![]() CE;
CE;
∵△ECG为等腰直角三角形,∴GC=![]() CE,∵GC=GB,∴GB=
CE,∵GC=GB,∴GB=![]() CE.
CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(x+2y)(x﹣2y)+(20xy3﹣8x2y2)÷4xy,其中x=2018,y=2019.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正数的平方根是a+3和2a﹣15,则这个数为 .
-
科目: 来源: 题型:
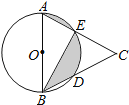
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
A.
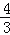 π﹣
π﹣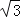 B.
B.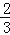 π C.
π C.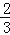 π﹣
π﹣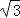 D.
D.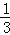 π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点F,点C与点E分别是对应点(如图所示),观察对应点与点的坐标之间的关系,解答下列问题:

(1)分别写出点A与点D,点B与点F,点C与点E的坐标
(2)若点P(a+9,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a3﹣4a=______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班第一小组7名同学的毕业升学体育测试成绩(满分30分)依次为:25,23,25,23,27,30,25,这组数据的中位数和众数分别是( )
A.23,25
B.23,23
C.25,23
D.25,25
相关试题

