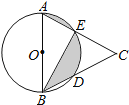
【题目】如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
A.![]() π﹣
π﹣![]() B.
B.![]() π C.
π C.![]() π﹣
π﹣![]() D.
D.![]() π
π
参考答案:
【答案】A
【解析】
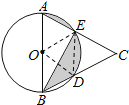
试题分析:已知D、E是半圆的三等分点,如果连接DE、OE、OD,那么△OAE、△ODE、△OBD、△CDE都是等边三角形,由此可求出扇形OBE的圆心角的度数和圆的半径长;由于∠AOE=∠BOD,则AB∥DE,S△ODE=S△BDE;可知阴影部分的面积=S扇形OAE﹣S△OAE+S扇形ODE求解.
解:连接OE、OD,点D、E是半圆的三等分点,
∴∠AOE=∠EOD=∠DOB=60°
∵OA=OE=OD=OB
∴△OAE、△ODE、△OBD、△CDE都是等边三角形,
∴AB∥DE,
∴S△ODE=S△BDE;
∴图中阴影部分的面积=S扇形OAE﹣S△OAE+S扇形ODE=![]() ×2﹣
×2﹣![]() =
=![]() π﹣
π﹣![]() .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店三月份盈利264000元,将264000用科学计数法表示应为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(x+2y)(x﹣2y)+(20xy3﹣8x2y2)÷4xy,其中x=2018,y=2019.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正数的平方根是a+3和2a﹣15,则这个数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,CD⊥AB于点D,CD=BD,BE平分∠ABC,点H是BC边的中点,连接DH,交BE于点G,连接CG.
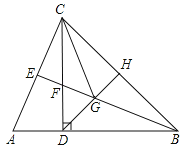
(1)求证:△ADC≌△FDB;
(2)求证:CE=
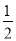 BF;
BF;(3)判断△ECG的形状,并证明你的结论;
(4)猜想BG与CE的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点F,点C与点E分别是对应点(如图所示),观察对应点与点的坐标之间的关系,解答下列问题:

(1)分别写出点A与点D,点B与点F,点C与点E的坐标
(2)若点P(a+9,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a3﹣4a=______________.
相关试题

