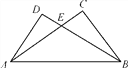
【题目】如图,在△ABC和△BAD中,AC与BD相交于点E,已知AD=BC,另外只能从下面给出的三个条件:①∠DAB=∠CBA;②∠D=∠C;③∠DBA=∠CAB中选择其中的一个用来证明△ABC和△BAD全等,这个条件是 (填序号),并证明△ABC≌△BAD.
参考答案:
【答案】①,证明见解析.
【解析】试题分析:分别针对所给的三个条件进行讨论,确定只有添加条件①,根据SAS即可证明△ABC≌△BAD.
试题解析:①添加条件∠DAB=∠CBA,还有已知条件AD=BC,AB是公共边,符合全等三角形的判定定理SAS,能推出△ABD≌△BAC,故①可以;
②添加条件∠D=∠C,还有已知条件AD=BC,AB是公共边,不符合全等三角形的判定定理,不能推出△ABD≌△BAC,故②不可以;
③添加条件∠DBA=∠CAB,还有已知条件AD=BC,AB是公共边,不符合全等三角形的判定定理,不能推出△ABD≌△BAC,故③不可以;
这个条件是①,证明如下:
在△ABD和△CBA中, 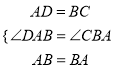 ,
,
∴△ABD≌△CBA(SAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0)下列说法:
①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(2,y2)是抛物线上的两点,则y1>y2 .
其中说法正确的是( )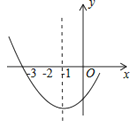
A.①②
B.②③
C.②③④
D.①②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFl,得到图②.
(1)在图①中,过点P作PM∥AB,当α=20°,β=50°时,∠EPM= 度,∠EPF= 度;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请直接写出α与β的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,取点D与点E,使得AD=AE,∠BAE=∠CAD,连结BD与CE交于点O.求证:

(1)△ABD≌△ACE;
(2)OB=OC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明
如图,端点为P的两条射线分别交两直线l1、l2于A、C、B、D四点,已知∠PBA=∠PDC,∠l=∠PCD,求证:∠2+∠3=180°.
证明:∵∠PBA=∠PDC( )
∴ (同位角相等,两直线平行)
∴∠PAB=∠PCD( )
∵∠1=∠PCD( )
∴ (等量代换)
∴PC//BF(内错角相等,两直线平行),
∴∠AFB=∠2( )
∵∠AFB+∠3=180°( )
∴∠2+∠3=180°(等量代换)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,AB=AC,O是BC的中点,如果在AB和AC上分别有一个动点M、N在移动,且在移动时保持AN=BM,请你判断△OMN的形状,并说明理由.

相关试题

