Question

【题目】如图，在△ABC中，AB=AC，取点D与点E，使得AD=AE，∠BAE=∠CAD，连结BD与CE交于点O．求证：

（1）△ABD≌△ACE；

（2）OB=OC．

Answer 1

【答案】见解析

【解析】

试题分析：（1）由已知条件得到∠BAD=∠CAE，根据全等三角形的判定定理即可得到结论；

（2）根据全等三角形的性质得到∠ABD=∠ACE，由等腰三角形的性质得到∠ABC=∠ACB由角的和差即可得到∠OBC=∠OCB，然后根据等腰三角形的判定即可得到结论．

证明：（1）∵∠BAE=∠CAD，

∴∠BAD=∠CAE，

在△ABD与△ACE中，，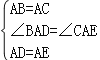

∴△ABD≌△ACE（SAS）；

（2）∵△ABD≌△ACE，

∴∠ABD=∠ACE，

∵AB=AC，

∴∠ABC=∠ACB

∴∠ABC﹣∠ABD=∠ACB﹣∠ACE，

即∠OBC=∠OCB，

∴OB=OC．