【题目】某兴趣小组为了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.请根据以上信息解答下列问题:
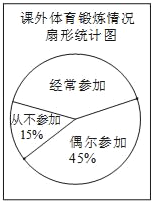

(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为_____;
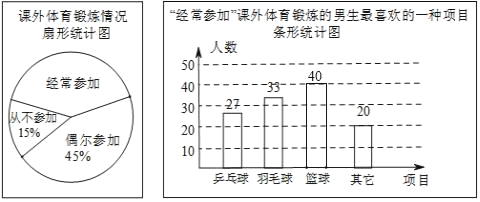
(2)请补全条形统计图;
(3)该校共有1000名男生,小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为1000×![]() =90”,请你判断这种说法是否正确,并说明理由.
=90”,请你判断这种说法是否正确,并说明理由.
(4)若要从被调查的“从不参加”课外体育锻炼的男生中随机选择10名同学组成课外活动小组,则从不参加活动的小王被选中的概率是多少?
参考答案:
【答案】144°
【解析】分析:(1)用“经常参加”所占的百分比乘以360°计算即可得解;
(2)先求出“经常参加”的人数,然后求出喜欢篮球的人数,再补全统计图即可;
(3)根据喜欢乒乓球的27人都是“经常参加”的学生,“偶尔参加”的学生中也会有喜欢乒乓球的考虑解答;
(4)求得从不参加的总人数,根据概率公式求解可得.
详解:(l)“经常参加”所对应的圆心角的度数为360°×(1﹣15%﹣45%)=144°,
故答案为:144°;
(2)经常参加的人数为300×(1﹣15%﹣45%)=120人,
则“篮球”选项的人数为120﹣(27+33+20)=40.
补全条形统计图如下:
(3)这种说法不正确.
理由如下:最喜欢兵乓球的人在“经常参加”课外活动的人中有27人,而在“偶尔参加”课外活动的人中也有可能有人喜欢兵乓球,
因此比例不一定是![]() ,
,
因此这种说法是错误的.
(4)∵从不参加的总人数为300×15%=45(人),
∴P(小王)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=x+1和x轴上,则点Bn的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=4cm,BC=6cm,∠B=60°,G是CD的中点,E是边AD上的动点(E不与A、D重合),且点E由A向D运动,速度为1cm/s,EG的延长线与BC的延长线交于点F,连接CE、DF,设点E的运动时间为
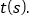
(1)求证:无论
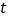 为何值,四边形CEDF都是平行四边形;
为何值,四边形CEDF都是平行四边形;(2)①当
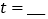 s时,CE⊥AD;
s时,CE⊥AD;②当
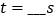 时,平行四边形CEDF的两条邻边相等.
时,平行四边形CEDF的两条邻边相等.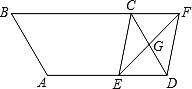
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知线段a、b
(1)求作一个等腰△ABC,使底边长BC=a,底边上的高为b.(尺规作图,只保留作图痕迹)
(2)小明由此想到一个命题:等腰三角形底边的中点到两腰的距离相等,请你判断这个命题的真假,如果是真命题请证明;如果是假命题请举出反例.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一块直角三角形的绿地,量得两直角边长分别为6m和8m,现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.

-
科目: 来源: 题型:
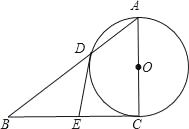
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线交BC于点E.
(1)求证:DE=
 BC;
BC;(2)若四边形ODEC是正方形,试判断△ABC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小亮、小刚、小颖一起研究一道数学题.如图,已知EF⊥AB,CD⊥AB.
小明说:“如果还知道∠CDG=∠BFE,那么能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连结GF,那么GF一定平行于AB.”
他们四人中,有________个人的说法是正确的.( )

A. 1 B. 2 C. 3 D. 4
相关试题

