【题目】反比例函数的图象经过点P(﹣1,2),则此反比例函数的解析式为 .
参考答案:
【答案】y=﹣ ![]()
【解析】解:设y= ![]() ,
,
∵图象经过点P(﹣1,2),
∴2= ![]() ,
,
解得:k=﹣2,
∴y关于x的解析式为y=﹣ ![]() ,
,
所以答案是:y=﹣ ![]() .
.
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点,以及对反比例函数的性质的理解,了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=A1B,在AA1的延长线上依次取A2、A3、A4、…、An,并依次在三角形的外部作等腰三角形,使A1C1=A1A2,A2C2=A2A3,A3C3=A3A4,…,An﹣1Cn﹣1=An﹣1An.
记∠BA1A=∠1,∠C1A2A1=∠2,……,以此类推. 若∠B=30°,则∠n=_________°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+2x﹣6与x轴交于点A(﹣6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.
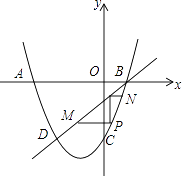
(1)连接CD,求抛物线的表达式和线段CD的长度;
(2)在线段BD下方的抛物线上有一点P,过点P作PM∥x轴,PN∥y轴,分别交BD于点M,N.当△MPN的面积最大时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
 +2sin60°﹣|﹣
+2sin60°﹣|﹣  |﹣(﹣2015)0 .
|﹣(﹣2015)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC是等边三角形,BD⊥AC,E是BC延长线上的一点,且∠CED=30°.
(1)求证:DB=DE.
(2)在图中过D作DF⊥BE交BE于F,若CF=3,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进冰箱、彩电进行销售,已知冰箱的进货单价比彩电的进货单价多400元,若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等.该商场冰箱、彩电的售货单价如下表:
冰箱
彩电
售价(元/台)
2500
2000
(1)分别求出冰箱、彩电的进货单价.
(2)为了满足市场需求,商场决定用不超过90 000元的资金采购冰箱、彩电共50台。若该商场将购进的冰箱、彩电共50台全部售出,获得利润为w元,为了使商场的利润最大,该商场该如何购进冰箱、彩电,最大利润是多少?
相关试题

